В МИРЕ НАУКИ. (Scientific American. Издание на русском языке). 1990. № 3

Искусственный интеллект:
различные взгляды
на проблему

Послвдние 35 лет попыток создать думающие машины были полны и удач, и разочарований. «Интеллектуальный» уровень современных компьютеров довольно высок, однако для того, чтобы компьютеры могли «разумно» вести себя в реальном мире, их поведенческие способности не должны уступать способностям по крайней мере самых примитивных животных. Некоторые специалисты, работающие в областях, не связанных с искусственным интеллектом, говорят, что компьютеры по своей природе не способны к сознательной умственной деятельности.

В этом нормере журнала в статье Дж.Р.Сирла утверждается, что компьютерные программы никогда не смогут достичь разума в привычном для нас понимании. В то же время в другой статье, написанной П.М.Черчлендом и П. С.Черчленд приводится мнение, что с помощью электронных схем, построенных по образу и подобию мозговых структур, возможно удастся создать искусственный интеллект. За этим спором по существу скрывается вопрос о том, что такое мышление. Этот вопрос занимал умы людей на протяжении тысячелетий. Практическая работа с компьютерами, которые пока не могут мыслить, породила новый взгляд на этот вопрос и отвергла многие потенциальные ответы на него. Остается найти правильный ответ.

Разум мозга — компьютерная программа?

Нет. Программа лишь манипулирует символами, мозг же придает им смысл

ДЖОН СИРЛ

СПОСОБНА ли машина мыслить? Может ли машина иметь сознанные мысли в таком же смысле, в каком имеем их мы? Если под машиной понимать физическую систему, способную выполнять определенные функции (а что еще под ней можно понимать?), тогда люди — это машины особой, биологической разновидности, а люди могут мыслить, и, стало быть, машины, конечно, тоже могут мыслить. Тогда, по всей видимости, можно создавать мыслящие машины из самых разнообразных материалов — скажем, из кремниевых кристаллов или электронных ламп. Если это и окажется невозможным, то пока мы, конечно, этого еще не знаем.

Однако в последние десятилетия вопрос о том, может ли машина мыслить, приобрел совершенно другую интерпретацию. Он был подменен вопросом: способна ли машина мыслить только за счет выполнения заложенной в нее компьютерной программы? Является ли программа основой мышления? Это принципиально иной вопрос, потому что он не затрагивает физических, каузальных (причинных) свойств существующих или возможных физических систем, а скорее относится к абстрактным, вычислительным свойствам формализованных компьютерных программ, которые могут быть реализованы в любом материале, лишь бы он был способен выполнять эти программы.

Довольно большое число специалистов по искусственному интеллекту (ИИ) полагают, что на второй вопрос следует ответить положительно; другими словами, они считают, что составив правильные программы с правильными входами и выходами, они действительно создадут разум. Более того, они полагают, что имеют в своем распоряжении научный тест, с помощью которого можно судить об успехе или неудаче такой попытки. Имеется в виду тест Тьюринга, изобретенный Аланом М. Тьюрингом, основоположником искусственного интеллекта. Тест Тьюринга в том смысле, как его сейчас понимают, заключается просто в следующем: если компьютер способен демонстрировать поведение, которое эксперт не сможет отличить от поведения человека, обладающего определенными мыслительными способностями (скажем, способностью вьшблнять операции сложения или понимать китайский язык), то компьютер также обладает этими способностями. Следовательно, цель заключается лишь в том, чтобы создать программы, способные моделировать человеческое мышление таким образом, чтобы выдерживать тест Тьюринга. Более того, такая программа будет не просто моделью разума; она в буквальном смысле слова сама и будет разумом, в том же смысле, в котором человеческий разум — это разум.

Конечно, далеко не каждый специалист по искусственному интеллекту разделяет такую крайнюю точку зрения. Более осторожный подход заключается в том, чтобы рассматривать компьютерные модели как полезное средство для изучения разума, подобно тому как они применяются при изучении погоды, пищеварения, экономики или механизмов молекулярной биологии. Чтобы провести различие между этими двумя подходами, я назову первый «сильным ИИ», а второй — «слабым ИИ». Важно понять, насколько радикальным является подход сильного ИИ. Сильный ИИ утверждает, что мышление — это не что иное, как манипулирование формализованными символами, а именно это и делает компьютер: он оперирует формализованными символами. Подобный взгляд часто суммируется примерно следующим высказыванием: «Разум по отношению к мозгу — это то же, что и программа по отношению к аппаратуре компьютера».

СИЛЬНЫЙ ИИ отличается от других теорий разума по крайней мере в двух отношениях: его можно четко сформулировать, но также четко и просто его можно опровергнуть. Характер этого опровержения таков, что каждый человек может попробовать провести его самостоятельно. Вот как это делается. Возьмем, например, какой-нибудь язык, которого вы не понимаете. Для меня таким языком является китайский. Текст, написанный по-китайски, я воспринимаю как набор бессмысленных каракулей. Теперь предположим, что меня поместили в комнату, в которой расставлены корзинки, полные китайских иероглифов. Предположим также, что мне дали учебник на английском языке, в котором приводятся правила сочетания символов китайского языка, причем правила эти можно применять, зная лишь форму символов, понимать значение символов совсем необязательно. Например, правила могут гласить: «Возьмите такой-то иероглиф из корзинки номер один и поместите его рядом с таким-то иероглифом из корзинки номер два».

Представим себе, что находящиеся за дверью комнаты люди, понимающие китайский язык, передают в комнату наборы символов и что в ответ я манипулирую символами согласно правилам и передаю обратно другие наборы символов. В данном случае книга правил есть не что иное, как «компьютерная программа». Люди, написавшие ее, — «программисты», а я играю роль «компьютера». Корзинки, наполненные символами, — это «база данных»; наборы символов, передаваемых в комнату, это «вопросы», а наборы, выходящие из комнаты, это «ответы».

Предположим далее, что книга правил написана так, что мои «ответы» на «вопросы» не отличаются от ответов человека, свободно владеющего китайским языком. Например, люди, находящиеся снаружи, могут передать непонятные мне символы, означающие; «Какой цвет вам больше всего нравится?» В ответ, выполнив предписанные правилами манипуляции, я выдам символы, к сожалению, мне также непонятные и означающие, что мой любимый цвет синий, но мне также очень нравится зеленый. Таким образом, я выдержу тест Тьюринга на понимание китайского языка. Но все же на самом деле я не понимаю ни слова по-китайски. К тому же я никак не могу научиться этому языку в рассматриваемой системе, поскольку не существует никакого способа, с помощью которого я мог бы узнать смысл хотя бы одного символа. Подобно компьютеру, я манипулирую символами, но не могу придать им какого бы то ни было смысла.

Сущность этого мысленного эксперимента состоит в следующем: если я не могу понять китайского языка только потому, что выполняю компьютерную программу для понимания китайского, то и никакой другой цифровой компьютер не сможет его понять таким образом. Цифровые компьютеры просто манипулируют формальными символами согласно правилам, зафиксированным в программе.

То, что касается китайского языка, можно сказать и о других формах знания. Одного умения манипулировать символами еще недостаточно, чтобы гарантировать знание, восприятие, понимание, мышление и т. д. И поскольку компьютеры как таковые — это устройства, манипулирующие символами, наличия компьютерной программы недостаточно, чтобы можно было говорить о наличии знания.

Этот простой аргумент имеет решающее значение для опровержения концепции сильного ИИ. Первая предпосылка аргумента просто констатирует формальный характер компьютерной программы. Программы определяются в терминах манипулирования символами, а сами символы носят чисто формальный, или «синтаксический» характер. Между прочим, именно благодаря формальной природе программы, компьютер является таким мощным орудием. Одна и та же программа может выполняться на машинах самой различной природы, равно как одна и та же аппаратная система способна выполнять самые разнообразные компьютерные программы. Представим это соображение кратко в виде «аксиомы»:

Аксиома 1. Компьютерные программы — это формальные (синтаксические) объекты.

Это положение настолько важно, что его стоит рассмотреть несколько подробнее. Цифровой компьютер обрабатывает информацию, сначала кодируя ее в символических обозначениях, используемых в машине, а затем манипулируя символами в соответствии с набором строго определенных правил. Эти правила представляют собой программу. Например, в рамках тьюринговской концепции компьютера в роли символов выступали просто 0 и 1, а правила программы предписывали такие операции, как «Записать 0 на ленте, продвинуться на одну ячейку влево и стереть 1». Компьютеры обладают удивительным свойством: любая представимая на естественном языке информация может быть закодирована в такой системе обозначений и любая задача по обработке информации может быть решена путем применения правил, которые можно запрограммировать.

ВАЖНОЕ значение имеют еще два момента. Во-первых, символы и программы — это чисто абстрактные понятия: они не обладают физическими свойствами, с помощью которых их можно было бы определить и реализовать в какой бы то ни было физической среде. Нули и единицы, как символы, не имеют физических свойств. Я акцентирую на этом внимание, поскольку иногда возникает соблазн отождествить компьютеры с той или иной конкретной технологией — скажем, с кремниевыми интегральными микросхемами — и считать, что речь идет о физических свойствах кремниевых кристаллов или что синтаксис означает какое-то физическое явление, обладающее, может быть, еще неизвестными каузальными свойствами аналогично реальным физическим явлениям, таким как электромагнитное излучение или атомы водорода, которые обладают физическими, каузальными свойствами. Второй момент заключается в том, что манипуляция символами осуществляется без всякой связи с каким бы то ни было смыслом. Символы в программе могут обозначать все, что угодно программисту или пользователю. В этом смысле программа обладает синтаксисом, но не обладает семантикой.

Следующая аксиома является простым напоминанием об очевидном факте, что мысли, восприятие, понимание и т. п. имеют смысловое содержание. Благодаря этому содержанию они могут служить отражением объектов и состояний реального мира. Если смысловое содержание связано с языком, то в дополнение к семантике, в нем будет присутствовать и синтаксис, однако лингвистическое понимание требует по крайней мере семантической основы. Если, например, я размышляю о последних президентских выборах, то мне в голову приходят определенные слова, но эти слова лишь потому относятся к выборам, что я придаю им специфическое смысловое значение в соответствии со своим знанием английского языка. В этом отношении они для меня принципиально отличаются от китайских иероглифов. Сформулируем это кратко в виде следующей аксиомы:

Аксиома 2. Человеческий разум оперирует смысловым содержанием (семантикой).

Теперь добавим еще один момент, который был продемонстрирован экспериментом с китайской комнатой. Располагать только символами как таковыми (т. е. синтаксисом) еще недостаточно для того, чтобы располагать семантикой. Простого манипулирования символами недостаточно, чтобы гарантировать знание их смыслового значения. Кратко представим это в виде аксиомы.

Аксиома 3. Синтаксис сам по себе не составляет семантику и его недостаточно для существования семантики.

На одном уровне этот принцип справедлив по определению. Конечно, кто-то может определить синтаксис и семантику по-иному. Главное, однако, в том, что существует различие между формальными элементами, не имеющими внутреннего смыслового значения, или содержания, и теми явлениями, у которых такое содержание есть. Из рассмотренных предпосылок следует:

Заключение 1. Программы не являются сущностью разума и их наличия недостаточно для наличия разума.

.

А это по существу означает, что утверждение сильного ИИ ложно.

Очень важно отдавать себе отчет в том, что именно было доказано с помощью этого рассуждения и что нет.

Во-первых, я не пытался доказывать, что «компьютер не может мыслить». Поскольку все, что поддается моделированию вычислениями, может быть описано как компьютер, и поскольку наш мозг на некоторых уровнях поддается моделированию, то отсюда тривиально следует, что наш мозг — это компьютер, и он, разумеется, способен мыслить. Однако из того факта, что систему можно моделировать посредством манипулирования символами и что она способна мыслить, вовсе не следует, что способность к мышлению эквивалентна способности к манипулированию формальными символами.

Во-вторых, я не пытался доказывать, что только системы биологической природы, подобные нашему мозгу, способны мыслить. В настоящее время это единственные известные нам системы, обладающие такой способностью, однако мы можем встретить во Вселенной и другие способные к осознанным мыслям системы, а может быть, мы даже сумеем искусственно создать мыслящие системы. Я считают этот вопрос открытым для споров.

В-третьих, утверждение сильного ИИ заключается не в том, что компьютеры с правильными программами могут мыслить, что они могут обладать какими-то неведомыми доселе психологическими свойствами; скорее, оно состоит в том, что компьютеры просто должны мыслить, поскольку их работа — это и есть не что иное, как мышление.

В-четвертых, я попытался опровергнуть сильный ИИ, определенный именно таким образом. Я пытался доказать, что мышление не сводится к программам, потому что программа лишь манипулирует формальными символами — а, как нам известно, самого по себе манипулирования символами недостаточно, чтобы гарантировать наличие смысла. Это тот принцип, на котором основано рассуждение о китайской комнате.

Я подчеркиваю здесь эти моменты отчасти потому, что П.М. и П.С.Черчленды в своей статье (см. Пол М. Черчленд и Патриция Смит Черчленд «Может ли машина мыслить?»), как мне кажется, не совсем правильно поняли суть моих аргументов. По их мнению, сильный ИИ утверждает, что компьютеры в конечном итоге могут обрести способность к мышлению и что я отрицаю такую возможность, рассуждая лишь на уровне здравого смысла. Однако сильный ИИ утверждает другое, и мои доводы против не имеют ничего общего со здравым смыслом.

Далее я скажу еще кое-что об их возражениях. А пока я должен заметить, что в противоположность тому, что говорят Черчленды, рассуждение с китайской комнатой опровергает любые утверждения сильного ИИ относительно новых параллельных технологий, возникших под влиянием и моделирующих работу нейронных сетей. В отличие от компьютеров традиционной архитектуры фон Неймана, работающих в последовательном пошаговом режиме, эти системы располагают многочисленными вычислительными элементами, работающими параллельно и взаимодействующими друг с другом в соответствии с правилами, основанными на открытиях нейробиологии. Хотя пока достигнуты скромные результаты, модели «параллельной распределенной обработки данных» или «коммутационные машины» подняли некоторые полезные вопросы относительно того, насколько сложными должны быть параллельные системы, подобные нашему мозгу, чтобы при их функционировании порождалось разумное поведение.

Однако параллельный, «подобный мозгу» характер обработки информации не является существенным для чисто вычислительных аспектов процесса. Любая функция, которая может быть вычислена на параллельной машине, будет вычислена и на последовательной. И действительно, ввиду того что параллельные машины еще редки, параллельные программы обычно все еще выполняются на традиционных последовательных машинах. Следовательно, параллельная обработка также не избегает аргумента, основанного на примере с китайской комнатой.

Более того, параллельные системы подвержены своей специфической версии первоначального опровергающего рассуждения в случае с китайской комнатой. Вместо китайской комнаты представьте себе китайский спортивный зал, заполненный большим числом людей, понимающих только английский язык. Эти люди будут выполнять те же самые операции, которые выполняются узлами и синапсами в машине коннекционной архитектуры, описанной Черчленда-ми, но результат будет тем же, что и в примере с одним человеком, который манипулирует символами согласно правилам, записанным в руководстве. Никто в зале не понимает ни слова по-китайски, и не существует способа, следуя которому вся система в целом могла бы узнать о смысловом значении хотя бы одного китайского слова. Тем не менее при правильных инструкциях эта система способна правильно отвечать на вопросы, сформулированные по-китайски.

У параллельных сетей, как я уже говорил, есть интересные свойства, благодаря которым они могут лучше моделировать мозговые процессы по сравнению с машинами с традиционной последовательной архитектурой. Однако преимущества параллельной архитектуры, существенные для слабого ИИ, не имеют никакого отношения к противопоставлению между аргументом, построенным на примере с китайской комнатой, и утверждением сильного ИИ. Черчленды упускают из виду этот момент, когда говорят, что достаточно большой китайский спортивный зал мог бы обладать более высокими умственными способностями, которые определяются размерами и степенью сложности системы, равно как и мозг в целом более «разумен», чем его отдельные нейроны. Возможно и так, но это не имеет никакого отношения к вычислительному процессу. С точки зрения выполнения вычислений последовательные и параллельные архитектуры совершенно идентичны: любое вычисление, которое может быть произведено в машине с параллельным режимом работы, может быть выполнено машиной с последовательной архитектурой. Если человек, находящийся в китайской комнате и производящий вычисления эквивалентен и той и другой системам, тогда, если он не понимает китайского языка исключительно потому, что ничего кроме вычислений не делает, то и эти системы также не понимают китайского языка. Черчленды правы, когда говорят, что первоначальный довод, основанный на примере с китайской комнатой, был сформулирован исходя из традиционного представления об ИИ, но они заблуждаются, считая что параллельная архитектура делает этот довод неуязвимым. Это справедливо в отношении любой вычислительной системы. Производя только формальные операции с символами (т. е. вычисления) вы не сможете обогатить свой разум семантикой, независимо от того выполняются эти вычислительные операции последовательно или параллельно; вот почему аргумент китайской комнаты опровергает сильный ИИ в любой его форме.

МНОГИЕ люди, на которых этот аргумент производит определенное впечатление, тем не менее затрудняются провести четкое различие между людьми и компьютерами. Если люди, по крайней мере в тривиальном смысле, являются компьютерами и если люди обладают семантикой, то почему они не могут наделить семантикой и другие компьютеры? Почему мы не можем запрограммировать компьютеры Vax или Cray таким образом, чтобы у них тоже появились мысли и чувства? Или почему какая-нибудь новая компьютерная технология не сможет преодолеть пропасть, разделяющую форму и содержание, или синтаксис и семантику? В чем на самом деле состоит то различие между биологическим мозгом и компьютерной системой, благодаря которому аргумент с китайской комнатой действует применительно к компьютерам, но не действует применительно к мозгу?

Наиболее очевидное различие заключается в том, что процессы, которые определяют нечто как компьютер (а именно вычислительные процессы), на самом деле совершенно не зависят от какого бы то ни было конкретного типа аппаратной реализации. В принципе можно сделать компьютер из старых жестяных банок из-под пива, соединив их проволокой и обеспечив энергией от ветряных мельниц.

Однако когда мы имеем дело с мозгом, то хотя современная наука в значительной степени еще пребывает в неведении относительно протекающих в мозгу процессов, мы поражаемся чрезвычайной специфичности анатомии и физиологии. Там, где мы достигли некоторого понимания того, как мозговые процессы порождают те или иные психические явления, — например, боль, жажду, зрение, обоняние — нам ясно, что в этих процессах участвуют вполне определенные нейробиологические механизмы. Чувство жажды, по крайней мере в некоторых случаях, обусловлено срабатыванием нейронов определенных типов в гипоталамусе, которое в свою очередь вызвано действием специфического пептида, ангиотензина II. Причинные связи прослеживаются здесь «снизу вверх» в том смысле, что нейронные процессы низшего уровня обусловливают психические явления на более высоких уровнях. В самом деле, каждое «ментальное» явление, от чувства жажды до мыслей о математических теоремах и воспоминаний о детстве, вызывается срабатыванием определенных нейронов в определенных нейронных структурах.

Однако почему эта специфичность имеет такое важное значение? В конце концов всевозможные срабатывания нейронов можно смоделировать на компьютерах, физические и химические свойства которых совершенно отличны от свойств мозга. Ответ состоит в том, что мозг не просто демонстрирует формальные процедуры или программы (он делает и это тоже), но и вызывает ментальные события благодаря специфическим нейробиологическим процессам. Мозг по сути своей является биологическим органом и именно его особые биохимические свойства позволяют достичь эффекта сознания и других видов ментальных явлений. Компьютерные модели мозговых процессов обеспечивают отражение лишь формальных аспектов этих процессов. Однако моделирование не следует смешивать с воспроизведением. Bычислительные модели ментальных процессов не ближе к реальности, чем вычислительные модели любого другого природного явления.

Можно представить себе компьютерную модель, отражающую воздействие пептидов на гипоталамус, которая будет точна вплоть до каждого отдельного синапса. Но с таким же успехом мы можем представить себе компьютерное моделирование процесса окисления углеводородов в автомобильном двигателе или пищеварительного процесса в желудке. И модель процессов, протекающих в мозге, ничуть не реальнее моделей, описывающих процессы сгорания топлива или пищеварительные процессы. Если не говорить о чудесах, то вы не сможете привести свой автомобиль в движение, моделируя на компьютере окисление бензина, и вы не сможете переварить обед, выполняя программу, которая моделирует пищеварение. Представляется очевидным и тот факт, что и моделирование мышления также не произведет нейробиологического эффекта мышления.

Следовательно, все ментальные явления вызываются нейробиологическими процессами мозга. Представим сокращенно этот тезис следующим образом:

Аксиома 4. Мозг порождает разум.

В соответствии с рассуждениями, приведенными выше, я немедленно прихожу к тривиальному следствию.

Заключение 2. Любая другая система, способная порождать разум, должна обладать каузальными свойствами (по крайней мере), эквивалентными соответствующим свойствам мозга.

Это равносильно, например, следующему утверждению: если электрический двигатель способен обеспечивать автомашине такую же высокую скорость, как двигатель внутреннего сгорания, то он должен обладать (по крайней мере) эквивалентной мощностью. В этом заключении ничего не говорится о механизмах. На самом деле, мышление — это биологическое явление: психические состояния и процессы обусловлены процессами мозга. Из этого еще не следует, что только биологическая система может мыслить, но это в то же время означает, что любая система другой природы, основанная на кремниевых кристаллах, жестяных банках и т. п., должна будет обладать каузальными возможностями, эквивалентными соответствующим возможностям мозга. Таким образом, я прихожу к следующему выводу:

Заключение 3. Любой артефакт, порождающий ментальные явления, любой искусственный мозг должен иметь способность вопроизводить специфические каузальные свойства мозга, и наличия этих свойств невозможно добиться только за счет выполнения формальной программы.

Более того, я прихожу к важному выводу, касающемуся человеческого мозга:

Заключение 4. Тот способ, посредством которого человеческий мозг на самом деле порождает ментальные явления, не может сводиться лишь к выполнению компьютерной программы.

.

ВПЕРВЫЕ сравнение с китайской комнатой было приведено мною на страницах журнала "Behavioral and Brain Sciences" (Науки о поведении и мозге) в 1980 г. Тогда моя статья сопровождалась, в соответствии с принятой в этом журнале практикой, комментариями оппонентов, в данном случае свои соображения высказали 26 оппонентов. Откровенно говоря, мне кажется, что смысл этого сравнения довольно очевиден, но, к моему удивлению, статья и в дальнейшем вызвала целый поток возражений, и что еще более удивительно, этот поток продолжается и по сей день. По-видимому, аргумент китайской комнаты затронул какое-то очень больное место.

Основной тезис сильного ИИ заключается в том, что любая система (независимо, сделана ли она из пивных банок, кремниевых кристаллов или просто из бумаги) не только способна обладать мыслями и чувствами, но просто должна ими обладать, если только она реализует правильно составленную программу, с правильными входами и выходами. Очевидно, это абсолютно антибиологическая точка зрения, и естественно было бы ожидать, что специалисты по искусственному интеллекту охотно откажутся от нее. Многие из них, особенно представители молодого поколения, согласны со мной, но меня поражает, как много сторонников имеет эта точка зрения и как настойчиво они защищают ее. Приведу некоторые наиболее распространенные из высказываемых ими доводов:

а) В китайской комнате вы на самом деле понимаете китайский, хотя и не отдаете себе в этом отчета. В конце концов вы можете понимать что-то и не отдавая себе в этом отчета.

б) Вы не понимаете китайского, но в вас существует подсистема (подсознание), которая понимает. Существуют ведь подсознательные психические состояния, и нет причины считать, что ваше понимание китайского не могло бы быть полностью неосознанным.

в) Вы не понимаете китайского, но комната как целое — понимает. Вы подобны отдельному нейрону в мозгу, и нейрон как таковой не может ничего понимать, он лишь вносит свой вклад в то понимание, которое демонстрирует система в целом; вы сами не понимаете, но вся система понимает.

г) Никакой семантики и не существует: есть только синтаксис. Полагать, что в мозгу есть какое-то загадочное «психическое содержание», «мыслительные процессы» или «семантика», это своего рода донаучная иллюзия. Все, что на самом деле существует в мозгу, — это некоторое синтаксическое манипулирование символами, которое осуществляется и в компьютерах. И ничего больше.

д) В действительности вы не выполняете компьютерную программу — это вам только кажется. Если существует некий сознательный агент, следующий строкам программы, то процесс уже вовсе не является простой реализацией программы.

е) Компьютеры обладали бы семантикой, а не только синтаксисом, если бы их входы и выходы были поставлены в причинные, каузальные зависимости — по отношению к остальному миру. Допустим, что мы снабдили робота компьютером, подключили телевизионные камеры к его голове, установили трансдьюсеры, подводящие телевизионную информацию к компьютеру, и позволили последнему управлять руками и ногами робота. В таком случае система как целое будет обладать семантикой.

ж) Если программа моделирует поведение человека, говорящего по-китайски, то она понимает китайский язык. Предположим, что нам удалось смоделировать работу мозга китайца на уровне нейронов. Но тогда, конечно, подобная система будет понимать китайский так же хорошо, как и мозг любого китайца.

И так далее.

У всех этих доводов есть одно общее свойство: все они неадекватны рассматриваемой проблеме, потому что не улавливают самой сути рассуждения о китайской комнате. Эта суть заключается в различии между формальным манипулированием символами, осуществляемым компьютером, и смысловым содержанием, биологически порождаемым мозгом, — различии, которое я для краткости выражения (и надеюсь, что это никого не введет в заблуждение) свел к различию между синтаксисом и семантикой. Я не буду повторять своих ответов на все эти возражения, однако проясню, возможно, ситуацию, если скажу, в чем заключаются слабости наиболее распространенного довода моих оппонентов, а именно довода (в), который я назову ответом системы. (Очень часто встречается также и довод (ж), основанный на идее моделирования мозга, но он уже был рассмотрен выше.)

В ОТВЕТЕ системы утверждается, что вы, конечно, не понимаете китайского, но вся система в целом — вы сами, комната, свод правил, корзинки, наполненные символами, — понимает. Когда я впервые услышал это объяснение, я спросил высказавшего это объяснение человека: «Вы что же, считаете, что комната может понимать китайский язык?» Он ответил, да. Это, конечно, смелое утверждение, однако, помимо того что оно совершенно неправдоподобно, оно не состоятельно еще и с чисто логической точки зрения. Суть моего исходного аргумента была в том, что простое тасование символов еще не обеспечивает доступа к пониманию смысла этих символов. Но это в той же мере касается комнаты в целом, как и находящегося в ней человека. В правоте моих слов можно убедиться, несколько расширив наш мысленный эксперимент. Представим себе, что я заучил наизусть содержимое корзинок и книги правил и что я провожу все вычисления в уме. Допустим даже, что я работаю не в комнате, а у всех на виду. В системе не осталось ничего такого, чего бы не было во мне самом, но поскольку я не понимаю китайского языка, не понимает его и система.

В своей статье мои оппоненты Черчленды используют одну из разновидностей ответа системы, придумав любопытную аналогию. Предположим, кто-то стал утверждать, что свет не может иметь электромагнитную природу, поскольку, когда человек перемещает магнит в темной комнате, мы не наблюдаем видимого светового излучения. Приведя этот пример, Черчленды спрашивают, а не является ли аргумент с китайской комнатой чем-то в том же роде? Не равносильно ли будет сказать, что когда вы манипулируете китайскими иероглифами в семантически темной комнате, в ней не возникает никакого просвета в понимании китайского языка? Но не может ли потом в ходе будущих исследований выясниться — так же, как было доказано, что свет все-таки целиком состоит из электромагнитного излучения, — что семантика целиком и полностью состоит из синтаксиса? Не является ли этот вопрос предметом дальнейшего научного изучения?

Аргументы, построенные на аналогиях, всегда очень уязвимы, поскольку, прежде чем аргумент станет состоятельным, необходимо еще убедиться, что две рассматриваемые ситуации действительно аналогичны. В данном случае, я думаю, что это не так. Объяснение света на основе электромагнитного излучения — это причинное рассуждение от начала и до конца. Это причинное объяснение физики электромагнитных волн. Однако аналогия с формальными символами не состоятельна, поскольку формальные символы не имеют физических причинных свойств. Единственное, что во власти символов как таковых, — это вызвать следующий шаг в программе, которую выполняет работающая машина. И здесь не возникает никакой речи о дальнейших исследованиях, которым еще предстоит раскрыть доселе неизвестные физические причинные свойства нулей и единиц. Последние обладают лишь одним видом свойств — абстрактными вычислительными свойствами, которые уже хорошо изучены.

Черчленды говорят, что у них «напрашивается вопрос», когда я утверждаю, что интерпретированные формальные символы не идентичны смысловому содержанию. Да, я, конечно, не тратил много времени на доказательство, что это так, поскольку я считаю это логической истиной. Как и в случае с любой другой логической истиной, каждый может быстро убедиться, что она справедлива, поскольку, предположив обратное, сразу приходишь к противоречию. Попробуем провести такое доказательство. Предположим, что в китайской комнате имеет место какое-то скрытое понимание китайского языка. Что же может превратить процесс манипулирования синтаксическими элементами в специфично китайское смысловое содержание? Подумав, я в конце концов пришел к выводу, что программисты должны были говорить по-китайски, коль скоро они сумели запрограммировать систему для обработки информации, представленной на китайском языке.

Хорошо. Но теперь представим себе, что надоело, сидя в китайской комнате, тасовать китайские (для меня бессмысленные) символы. Предположим, мне пришло в голову интерпретировать эти символы как обозначения ходов в шахматной игре. Какой семантикой теперь обладает система? Обладает ли она китайской семантикой или шахматной, или она обладает одновременно и той и другой? Предположим, что есть еще некая третья личность, наблюдающая за мной в окошко, и она решает, что мое манипулирование символами можно интерпретировать как предсказание курса акций на бирже. И так далее. Не существует предела количеству семантических интерпретаций, которое можно приписать символам, поскольку, я повторяю, символы носят чисто формальный характер. Они не содержат в себе внутренней семантики.

Можно ли каким-то образом спасти аналогию Черчлендов? Выше я сказал, что формальные символы не имеют каузальных свойств. Но, конечно, программа всегда выполняется той или иной конкретной аппаратурой, и эта аппаратура обладает своими специфическими физическими, каузальными свойствами. Любой реальный компьютер порождает различные физические явления. Мой компьютер, к примеру, выделяет тепло, производит монотонный шум и т. д. Существует ли здесь какое-либо строгое логическое доказательство, что компьютер не может производить аналогичным образом эффект сознания? Нет. В научном смысле об этом и речи быть не может, однако это совсем не то, что призвано опровергать рассуждение о китайской комнате, и не то, на чем будут настаивать сторонники сильного ИИ, поскольку любой производимый таким образом эффект будет достигать за счет физических свойств реализующей программу среды. Основное утверждение сильного ИИ заключается в том, что физические свойства реализующей среды не имеют никакого значения. Имеют значение лишь программы, а программы — это чисто формальные объекты.

Таким образом аналогия Черчлендов между синтаксисом и электромагнитным излучением наталкивается на дилемму: либо синтаксис следует понимать чисто формально, через его абстрактные математические свойства, либо нет. Если выбрать первую альтернативу, то аналогия становится несостоятельной, поскольку синтаксис, понимаемый таким образом, не имеет физических свойств. Если же, с другой стороны, рассматривать синтаксис в плоскости физических свойств реализующей среды, тогда аналогия действительно состоятельна, но она не имеет отношения к сильному ИИ.

ПОСКОЛЬКУ сделанные мною утверждения довольно очевидны — синтаксис это не то же самое, что семантика; мозговые процессы порождают психические явления — возникает вопрос, а как вообще возникла эта путаница? Кому могло прийти в голову, что компьютерное моделирование ментального процесса полностью ему идентично? В конце концов весь смысл моделей заключается в том, что они улавливают лишь какую-то часть моделируемого явления и не затрагивают остального. Ведь никто не думает, что мы-захотим поплавать в бассейне, наполненном шариками для пинг-понга, моделирующими молекулы воды. Можно ли тогда считать, что компьютерная модель мыслительных процессов на самом деле способна мыслить?

Отчасти эти недоразумения объясняются тем, что люди унаследовали некоторые положения -бихевиористских психологических теорий прошлого поколения. Под тестом Тьюринга скрывается соблазн считать, что если нечто ведет себя так, как будто оно обладает ментальными процессами, то оно и на самом деле должно ими обладать. Частью ошибочной бихевиористской концепции было также и то, что психология, для того чтобы оставаться научной дисциплиной, должна ограничиваться изучением внешне наблюдаемого поведения. Парадоксально, но этот остаточный бихевиоризм связан с остаточным дуализмом. Никто не думает, что компьютерная модель пищеварения способна что-то переварить на самом деле, но там, где речь идет о мышлении, люди охотно верят в такие чудеса, потому что забывают о том, что разум — это такое же биологическое явление, как и пищеварение. По их мнению, разум — это нечто формальное и абстрактное, а вовсе не часть полужидкой субстанции, из которой состоит наш головной мозг. Полемическая литература по искусственному интеллекту обычно содержит нападки на то, что авторы называют дуализмом, но при этом они не замечают, как сами демонстрируют ярко выраженный дуализм, поскольку если не принять точку зрения, что разум совершенно не зависит от мозга или какой-либо другой физически специфической системы, то следует считать невозможным создание разума только за счет написания программ.

Исторически в странах Запада научные концепции, в которых люди рассматривались как часть обычного физического или биологического мира, часто встречали противодействие со стороны реакции. Идеям Коперника и Галилея противились, потому что они отрицали, что Земля является центром Вселенной. Против Дарвина выступали потому, что он утверждал, что люди произошли от низших животных. Сильный ИИ правильнее всего было бы рассматривать как одно из последних проявлений этой антинаучной традиции, так как он отрицает, что человеческий разум содержит что-то существенно физическое или биологическое. Согласно утверждениям сильного ИИ, разум не зависит от мозга. Он представляет собой компьютерную программу и по существу не связан ни с какой специфической аппаратурой.

Многие люди, сомневающиеся относительно физической значимости искусственного интеллекта, полагают, что компьютеры, может быть, и смогут понимать китайский язык или думать о числах, но принципиально не способны на проявления чисто человеческих свойств, а именно (и далее следует их излюбленная человеческая специфика): любовь, чувство юмора, тревога за судьбу постиндустриального общества в эпоху современного капитализма и т. д. Но специалисты по ИИ справедливо настаивают, что эти возражения не корректны, что здесь как бы отодвигаются футбольные ворота. Если искусственное моделирование интеллекта окажется успешным, то психологические вопросы уже не имеют сколь-нибудь важного значения, В этом споре обе стороны не замечают различия между моделированием и воспроизведением. Пока речь идет о моделировании, то не стоит никакого труда запрограммировать мой компьютер, чтобы он напечатал: «Я люблю тебя, Сюзи»; «Ха-ха!» или «Я испытываю тревоги постиндустриального общества». Важно отдавать себе отчет в том, что моделирование — это не то же самое, что воспроизведение; и этот факт имеет такое же отношение к размышлениям об арифметике, как и к чувству тревоги. Дело не в том, что компьютер доходит только до центра поля и не доходит до ворот. Компьютер даже не трогается с места. Он просто не играет в эту игру.

Искусственный интеллект:
Может ли машина мыслить?

Классический искусственный интеллект едва ли будет воплощен в мыслящих машинах; предел человеческой изобретательности в этой области, по-видимому, ограничится созданием систем, имитирующих работу мозга

ПОЛ М. ЧЕРЧЛЕНД, ПАТРИЦИЯ СМИТ ЧЕРЧЛЕНД

В НАУКЕ об искусственном интеллекте (ИИ) происходит революция. Чтобы объяснить ее причины и смысл и представить рассуждения Джона Р. Сирла в перспективе, мы прежде должны обратиться к истории.

В начале 50-х годов традиционный, несколько расплывчатый вопрос о том, может ли машина мыслить, уступил более доступному вопросу: может ли мыслить машина, манипулирующая физическими символами в соответствии с правилами, учитывающими их структуру. Этот вопрос сформулирован точнее, потому что за предшествовавшие полвека формальная логика и теория вычислений существенно продвинулись вперед. Теоретики стали высоко оценивать возможности абстрактных систем символов, которые претерпевают преобразования в соответствии с определенными правилами. Казалось, что если эти системы удалось бы автоматизировать, то их абстрактная вычислительная мощь проявилась бы в реальной физической системе. Подобные взгляды способствовали рождению вполне определенной программы исследований на достаточно глубокой теоретической основе.

Может ли машина мыслить? Было много причин для того, чтобы ответить да. Исторически одна из первых и наиболее глубоких причин заключалась в двух важных результатах теории вычислений. Первый результат был тезисом Черча, согласно которому каждая эффективно вычислимая функция является рекурсивно вычислимой. Термин «эффективно вычислимая» означает, что существует некая «механическая» процедура, с помощью которой можно за конечное время вычислить результат при заданных входных данных. «Рекурсивно вычислимая» означает, что существует конечное множество операций, которые можно применить к заданному входу, а затем последовательно и многократно применять к вновь получаемым результатам, чтобы вычислить функцию за конечное время. Понятие механической процедуры не формальное, а скорее интуитивное, и потому тезис Черча не имеет формального доказательства. Однако он проникает в самую суть того, чем является вычисление, и множество различных свидетельств сходится в его подтверждение.

Второй важный результат был получен Аланом М. Тьюрингом, продемонстрировавшим, что любая рекурсивно вычислимая функция может быть вычислена за конечное время с помощью максимально упрощенной машины, манипулирующей символами, которую позднее стали называть универсальной машиной Тьюринга. Эта машина управляется рекурсивно применимыми правилами, чувствительными к идентичности, порядку и расположению элементарных символов, которые играют роль входных данных.

ИЗ ЭТИХ двух результатов вытекает очень важное следствие, а именно что стандартный цифровой компьютер, снабженный правильной программой, достаточно большой памятью и располагающий достаточным временем, может вычислить любую управляемую правилами функцию с входом и выходом. Другими словами, он может продемонстрировать любую систематическую совокупность ответов на произвольные воздействия со стороны внешней среды.

Конкретизируем это следующим образом: рассмотренные выше результаты означают, что соответственно запрограммированная машина, манипулирующая символами (в дальнейшем будем называть ее МС-машиной), должна удовлетворять тесту Тьюринга на наличие сознательного разума. Тест Тьюринга — это чисто бихевиористский тест, тем не менее его требования очень сильны. (Насколько состоятелен этот тест, мы рассмотрим ниже, там где встретимся со вторым, принципиально отличным «тестом» на наличие сознательного разума.) Согласно первоначальной версии теста Тьюринга, входом для МС-машины должны быть вопросы и фразы на естественном разговорном языке, которые мы набираем на клавиатуре устройства ввода, а выходом являются ответы МС-машины, напечатанные устройством вывода. Считается, что машина выдержала этот тест на присутствие сознательного разума, если ее ответы невозможно отличить от ответов, напечатанных реальным, разумным человеком. Конечно, в настоящее время никому не известна та функция, с помощью которой можно было бы получить выход, не отличающийся от поведения разумного человека. Но результаты Черча и Тьюринга гарантируют нам, что какова бы ни была эта (предположительно эффективная) функция, МС-машина соответствующей конструкции сможет ее вычислить.

Это очень важный вывод, особенно если учесть, что тьюринговское описание взаимодействия с машиной при помощи печатающей машинки представляет собой несущественное ограничение. То же заключение остается в силе, даже если МС-машина взаимодействует с миром более сложными способами: с помощью аппарата непосредственного зрения, естественной речи и т. д. В конце концов более сложная рекурсивная функция все же остается вычислимой по Тьюрингу. Остается лишь одна проблема: найти ту несомненно сложную функцию, которая управляет ответными реакциями человека на воздействия со стороны внешней среды, а затем написать программу (множество рекурсивно применимых правил), с помощью которой МС-машина вычислит эту функцию. Вот эти цели и легли в основу научной программы классического искусственного интеллекта.

Первые результаты были обнадеживающими. МС-машины с остроумно составленными программами продемонстрировали целый ряд действий, которые как будто относятся к проявлениям разума. Они реагировали на сложные команды, решали трудные арифметические, алгебраические и тактические задачи, играли в шашки и шахматы, доказывали теоремы и поддерживали простой диалог. Результаты продолжали улучшатьсгя с появлением более емких запоминающих устройств, более быстродействующих машин, а также с разработгюй более мощных и изощренных программ. Классический, или «построенный на программировании», ИИ представлял собой очень живое и успешное научное направление почти со всех точек зрения. Периодически высказывавшееся отрицание того, что МС-машины в конечном итоге будут способны мыслить, казалось проявлением необъективности и неинформированности. Свидетельства в пользу положительного ответа на вопрос, вынесенный в заголовок статьи, казались более чем убедительными.

Конечно, оставались кое-какие неясности. Прежде всего МС-машины не очень-то напоминали человеческий мозг. Однако и здесь у классического ИИ был наготове убедительный ответ. Во-первых, физический материал, из которого сделана МС-машина, по существу не имеет никакого отношения к вычисляемой ею функции. Последняя зафиксирована в программе. Во-вторых, техничекие подробности функциональной архитектуры машины также не имеют значения, поскольку совершенно различные архитектуры, рассчитанные на работу с совершенно различными программами, могут тем не менее выполнять одну и ту же функцию по входу-выходу.

Поэтому целью ИИ было найти функцию, по входу и выходу характерную для разума, а также создать наиболее эффективную из многих возможных программ для того, чтобы вычислить эту функцию. При этом говорили, что тот специфичный способ, с помощью которого функция вычисляется человеческим мозгом, не имеет значения. Этим и завершается описание сущности классического ИИ и оснований для положительного ответа на вопрос, поставленный в заголовке статьи.

МОЖЕТ ЛИ машина мыслить? Были также кое-какие доводы и в пользу отрицательного ответа. На протяжении 60-х годов заслуживающие внимания отрицательные аргументы встречались относительно редко. Иногда высказывалось возражение, заключающееся в том, что мышление — это не физический процесс и протекает он в нематериальной душе. Однако подобное дуалистическое воззрение не выглядело достаточно убедительным ни с эволюционной, ни с логической точки зрения. Оно не оказало сдерживающего влияния на исследования в области ИИ.

Гораздо большее внимание специалистов по ИИ привлекли соображения иного характера. В 1972 г. Хьюберт Л. Дрейфус опубликовал книгу, в которой резко критиковались парадные демонстрации проявлений разума у систем ИИ. Он указывал на то, что эти системы не адекватно моделировали подлинное мышление, и вскрыл закономерность, присущую всем этим неудачным попыткам. По его мнению, в моделях отсутствовал тот огромный запас неформализованных общих знаний о мире, которым располагает любой человек, а также способность, присущая здравому рассудку, опираться на те или иные составляющие этих знаний,в зависимости от требований изменяющейся обстановки. Дрейфус не отрицал принципиальной возможности создания искусственной физичесгсой системы, способной мыслить, но он весьма критически отнесся к идее о том, что это может быть достигнуто только за счет манипулирования символами с помощью рекурсивно применяемых правил.

В кругах специалистов по искусственному интеллекту, а также философов рассуждения Дрейфуса были восприняты главным образом как недальновидные и необъективные, базирующиеся на неизбежных упрощениях, присущих этой еще очень молодой области исследований. Возможно, указанные недостатки действительно имели место, но они, конечно, были временными. Настанет время, когда более мощные машины и более качественные программы позволят избавиться от этих недостатков. Казалось, что время работает на искусственный интеллект. Таким образом, и эти возражения не оказали сколько-нибудь заметного влияния на дальнейшие исследования в области ИИ.

Однако оказалось, что время работало и на Дрейфуса: в конце 70-х - начале 80-х годов увеличение быстродействия и объема памяти компьютеров повышало их «умственные способности» ненамного. Выяснилось, например, что распознавание образов в системах машинного зрения требует неожиданно большого объема вычислений. Для получения практически достоверных результатов нужно было затрачивать все больше и больше машинного времени, намного превосходя время, требуемое для выполнения тех же задач биологической системе зрения. Столь медленный процесс моделирования настораживал: ведь в компьютере сигналы распространяются приблизительно в миллион раз быстрее, чем в мозге, а тактовая частота центрального процессорного устройства компьютера примерно во столько же раз выше частоты любых колебаний, обнаруженных в мозге. И все же на реалистических задачах черепаха легко обгоняет зайца.

Кроме того, для решения реалистических задач необходимо, чтобы компьютерная программа обладала доступом к чрезвычайно обширной базе данных. Построение такой базы данных уже само по себе представляет довольно сложную проблему, но она усугубляется еще одним обстоятельством: каким образом обеспечить доступ к конкретным, зависящим от контекста фрагментам этой базы данных в реальном масштабе времени. По мере того как базы данных становились все более емкими, проблема доступа осложнялась. Исчерпывающий поиск занимал слишком много времени, а эвристические методы не всегда приводили к успеху. Опасения, подобные тем, что высказывал Дрейфус, начали разделять даже некоторые специалисты, работающие в области искусственного интеллекта.

Приблизительно в это время (1980 г.) Джон Сирл высказал принципиально новую критическую концепцию, ставившую под сомнение само фундаментальное предположение классической программы исследований по ИИ, а именно - идею о том, что правильное манипулирование структурированными символами путем рекурсивного применения правил, учитывающих их структуру, может составлять сущность сознательного разума.

Основной аргумент Сирла базировался на мысленном эксперименте, в котором он демонстрирует два очень важных обстоятельства. Во-первых, он описывает МС-машину, которая (как мы должны понимать) реализует функцию, по входу и выходу способную выдержать тест Тьюринга в виде беседы, протекающей исключительно на китайском языке. Во-вторых, внутренняя структура машины такова, что независимо от того, какое поведение она демонстрирует, у наблюдателя не возникает сомнений в том, что ни машина в целом, ни любая ее часть не понимают китайского языка. Все, что она в себе содержит, - это говорящий только по-английски человек, выполняющий записанные в инструкции правила, с помощью которых следует манипулировать символами, входящими и выходящими через окошко для почтовой корреспонденции в двери. Короче говоря, система положительно удовлетворяет тесту Тьюринга, несмотря на то что не обладает подлинным пониманием китайского языка и реального семантического содержания сообщений (см. статью Дж. Сирла «Разум мозга - компьютерная программа?»).

Отсюда делается общий вывод, что любая система, просто манипулирующая физическими символами согласно чувствительным к структуре правилам, будет в лучшем случае лишь жалкой пародией настоящего сознательного разума, поскольку невозможно породить «реальную семантику», просто крутя ручку «пустого синтаксиса». Здесь следует заметить, что Сирл выдвигает не бихевиористский (не поведенческий) тест на наличие сознания: элементы сознательного разума должны обладать реальным семантическим содержанием.

Возникает соблазн упрекнуть Сирла в том, что его мысленный эксперимент не адекватен, поскольку предлагаемая им система, действующая по типу «кубика-рубика», будет работать до абсурда медленно. Однако Сирл настаивает, что быстродействие в данном случае не играет никакой роли. Думающий медленно все же думает верно. Все необходимое для воспроизведения мышления, согласно концепции классического ИИ, по его мнению, присутствует в «китайской комнате».

Статья Сирла вызвала оживленные отклики специалистов по ИИ, психологов и философов. Однако в общем и целом она была встречена еще более враждебно, чем книга Дрейфуса. В своей статье, которая одновременно публикуется в этом номере журнала, Сирл приводит ряд критических доводов, высказываемых против его концепции. По нашему мнению, многие из них правомерны, в особенности те, авторы которых жадно «кидаются на приманку», утверждая, что, хотя система, состоящая из комнаты и ее содержимого, работает ужасно медленно, она все же понимает китайский язык.

Нам нравятся эти ответы, но не потому, что мы считаем, будто китайская комната понимает китайский язык. Мы согласны с Сирлом, что она его не понимает. Привлекательность этих аргументов в том, что они отражают отказ воспринять важнейшую третью аксиому в рассуждении Сирла: « Синтаксис сам по себе не составляет семантику и его недостаточно для существования семантики». Возможно, эта аксиома и справедлива, но Сирл не может с полным основанием утверждать, что ему это точно известно. Более того, предположить, что она справедлива, - значит напрашиваться на вопрос о том, состоятельна ли программа исследований классического ИИ, поскольку эта программа базируется на очень интересном предположении, что если нам только удастся привести в движение соответствующим образом структурированный процесс, своеобразный внутренний танец синтаксических элементов, правильно связанный со входами и выходами, то мы можем получить те же состояния и проявления разума, которые присущи человеку.

То, что третья аксиома Сирла действительно напрашивается на этот вопрос, становится очевидно, когда мы непосредственно сопоставляем ее с его же первым выводом: «Программы появляются сущностью разума и их наличия не достаточно для наличия разума». Не трудно видеть, что его третья аксиома уже несет в себе 90% почти идентичного ей заключения. Вот почему мысленный эксперимент Сирла специально придуман для того, чтобы подкрепить третью аксиому. В этом вся суть китайской комнаты.

Хотя пример с китайской комнатой делает аксиому 3 привлекательной для непосвященного, мы не думаем, что он доказывает справедливость этой аксиомы, и чтобы продемонстрировать несостоятельность этого примера, мы предлагаем в качестве иллюстрации свой параллельный пример. Часто один удачный пример, опровергающий оспариваемое утверждение, значительно лучше проясняет ситуацию, чем целая книга, полная логического жонглирования.

В истории науки было много примеров скепсиса, подобного тому, который мы видим в рассуждениях Сирла. В XVIII в. ирландский епископ Джордж Беркли считал немыслимым, чтобы волны сжатия в воздухе сами по себе могли быть сущностью звуковых явлений или фактором, достаточным для их существования. Английский поэт и художник Уильям Блейк и немецкий поэт-естествоиспытатель Иоган Гете считали немыслимым, чтобы маленькие частички материи сами по себе могли быть сущностью или фактором, достаточным для объективного существования света. Даже в нынешнем столетии находились люди, которые не могли себе вообразить, чтобы неодушевленная материя сама по себе, независимо от того, насколько сложна ее организация, могла быть органической сущностью или достаточным условием жизни. Совершенно очевидно то, что люди могут или не могут себе представить, зачастую никак не связано с тем, что на самом деле существует или не существует в действительности. Это справедливо, даже когда речь идет о людях с очень высоким уровнем интеллекта.

Чтобы увидеть, каким образом эти исторические уроки можно применить к рассуждениям Сирла, применим искусственно придуманную параллель к его логике и подкрепим эту параллель мысленным экспериментом.

Аксиома 1. Электричество и магнетизм - это физические силы.

Аксиома 2. Существенное свойство света - это свечение.

Аксиома 3. Силы сами по себе появляются сущностью эффекта свечения и не достаточны для его наличия.

Заключение 1. Электричество и магнетизм не являются сущностью света и не достаточны для его наличия.

Предположим, что это рассуждение было опубликовано вскоре после того, как Джеймс К. Максвелл в 1864 г. высказал предположение, что свет и электромагнитные волны идентичны, но до того как в мире были полностью осознаны систематические параллели между свойствами света и свойствами электромагнитных волн. Приведенное выше логическое рассуждение могло показаться убедительным возражением против смелой гипотезы Максвелла, в особенности если бы оно сопровождалось следующим комментарием в поддержку аксиомы 3.

«Рассмотрим темную комнату, в которой находится человек, держащий в руках постоянный магнит или заряженный предмет. Если человек начнет перемещать магнит вверх-вниз, то, согласно теории Максвелла об искусственном освещении (ИО), от магнита будет исходить распространяющаяся сфера электромагнитных волн и в комнате станет светлее. Но, как хорошо известно всем, кто пробовал играть с магнитами или заряженными шарами, их силы (а если на то пошло, то и любые другие силы), даже когда эти объекты приходят в движение, не создают никакого свечения. Поэтому представляется немыслимым, чтобы мы могли добиться реального эффекта свечения просто за счет манипулирования силами!»

КОЛЕБАНИЯ ЭЛЕКТРОМАГНИТНЫХ СИЛ представляют собой свет, хотя магнит, который перемещает человек, не производит никакого свечения. Аналогично манипулирование символами в соответствии с определенными правилами может представлять собой разум, хотя у основанной на применении правил системы, находящейся в «китайской комнате» Дж. Сирла, настоящее понимание как будто отсутствует.

Что же мог ответить Максвелл, если бы ему был брошен этот вызов?

Во-первых, он, возможно, стал бы настаивать на том, что эксперимент со «светящейся комнатой» вводит нас в заблуждение относительно свойств видимого света, потому что частота колебаний магнита крайне мала, меньше, чем нужно, приблизительно в 10¹⁵ раз. На это может последовать нетерпеливый ответ, что частота здесь не играет никакой роли, что комната с колеблющимся магнитом уже содержит все необходимое для проявления эффекта свечения в полном соответствии с теорией самого Максвелла.

В свою очередь Максвелл мог бы «проглотить приманку», заявив совершенно обоснованно, что комната уже полна свечения, но природа и сила этого свечения таковы, что человек не способен его видеть. (Из-за низкой частоты, с которой человек двигает магнитом, длина порождаемых электромагнитных волн слишком велика, а интенсивность слишком мала, чтобы глаз человека мог на них среагировать.) Однако, учитывая уровень понимания этих явлений в рассматриваемый период времени (60-е годы прошлого века), такое объяснение, вероятно, вызвало бы смех и издевательские реплики. «Светящаяся комната! Но позвольте, мистер Максвелл, там же совершенно темно!»

Итак, мы видим, что бедному Максвеллу приходится туго. Все, что он может сделать, это настаивать на следующих трех положениях. Во-первых, аксиома 3 в приведенном выше рассуждении не верна. В самом деле, несмотря на то что интуитивно она выглядит достаточно правдоподобной, по ее поводу у нас невольно возникает вопрос. Во-вторых, эксперимент со светящейся комнатой не демонстрирует нам ничего интересного относительно физической природы света. И в-третьих, чтобы на самом деле решить проблему света и возможности искусственного свечения, нам необходима программа исследований, которая позволит установить, действительно ли при соответствующих условиях поведение электромагнитных волн полностью идентично поведению света.

Такой же ответ должен дать классический искусственный интеллект на рассуждение Сирла. Хотя китайская комната Сирла и может показаться «в семантическом смысле темной», у него нет достаточных оснований настаивать, что совершаемое по определенным правилам манипулирование символами никогда не сможет породить семантических явлений, в особенности если учесть, что люди еще плохо информированы и ограничены лишь пониманием на уровне здравого смысла тех семантических и мыслительных явлений, которые нуждаются в объяснении. Вместо того чтобы воспользоваться пониманием этих вещей, Сирл в своих рассуждениях свободно пользуется отсутствием у людей такого понимания.

Высказав свои критические замечания по поводу рассуждений Сирла, вернемся к вопросу о том, имеет ли программа классического ИИ реальный шанс решить проблему сознательного разума и создать мыслящую машину. Мы считаем, что перспективы здесь не блестящие, однако наше мнение основано на причинах, в корне отличающихся от тех аргументов, которыми пользуется Сирл. Мы основываемся на конкретных неудачах исследовательской программы классического ИИ и на ряде уроков, преподанных нам биологическим мозгом на примере нового класса вычислительных моделей, в которых воплощены некоторые свойства его структуры. Мы уже упоминали о неудачах классического ИИ при решении тех задач, которые быстро и эффективно решаются мозгом. Ученые постепенно приходят к общему мнению о том, что эти неудачи объясняются свойствами функциональной архитектуры МС-машин, которая просто непригодна для решения стоящих перед ней сложных задач.

ЧТО НАМ нужно знать, так это каким образом мозг достигает эффекта мышления? Обратное конструирование является широко распространенным приемом в технике. Когда в продажу поступает какое-то новое техническое устройство, конкуренты выясняют, каким образом оно работает, разбирая его на части и пытаясь угадать принцип, на котором оно основано. В случае мозга реализация такого подхода оказывается необычайно трудной, поскольку мозг представляет собой самую сложную вещь на планете. Тем не менее нейрофизиологам удалось раскрыть многие свойства мозга на различных структурных уровнях. Три анатомические особенности принципиально отличают его от архитектуры традиционных электронных компьютеров.

Во-первых, нервная система - это параллельная машина, в том смысле, что сигналы обрабатываются одновременно на миллионах различных путей. Например, сетчатка глаза передает сложный входной сигнал мозгу не порциями по 8,16 или 32 элемента, как настольный компьютер, а в виде сигнала, состоящего почти из миллиона отдельных элементов, прибывающих одновременно к окончанию зрительного нерва (наружному коленчатому телу), после чего они также одновременно, в один прием, обрабатываются мозгом. Во-вторых, элементарное «процессорное устройство» мозга, нейрон, отличается относительной простотой. Кроме того, его ответ на входной сигнал - аналоговый, а не цифровой, в том смысле, что частота выходного сигнала изменяется непрерывным образом в зависимости от входных сигналов.

В-третьих, в мозге, кроме аксонов, ведущих от одной группы нейронов к другой, мы часто находим аксоны, ведущие в обратном направлении. Эти возвращающиеся отростки позволяют мозгу модулировать характер обработки сенсорной информации. Еще важнее то обстоятельство, что благодаря их существованию мозг является подлинно динамической системой, у которой непрерывно поддерживаемое поведение отличается как очень высокой сложностью, так и относительной независимостью от периферийных стимулов. Полезную роль в изучении механизмов работы реальных нейронных сетей и вычислительных свойств параллельных архитектур в значительной мере сыграли упрощенные модели сетей. Рассмотрим, например, трехслойную модель, состоящую из нейроноподобных элементов, имеющих аксоноподобные связи с элементами следующего уровня. Входной стимул достигает порога активации данного входного элемента, который посылает сигнал пропорциональной силы по своему «аксону» к многочисленным «синаптическим» окончаниям элементов скрытого слоя. Общий эффект заключается в том, что та или иная конфигурация активирующих сигналов на множестве входных элементов порождает определенную конфигурацию сигналов на множестве скрытых элементов.

То же самое можно сказать и о выходных элементах. Аналогичным образом конфигурация активирующих сигналов на срезе скрытого слоя приводит к определенной картине активации на срезе выходных элементов. Подводя итог, можно сказать, что рассматриваемая сеть является устройством для преобразования любого большого количества возможных входных векторов (конфигураций активирующих сигналов) в однозначно соответствующий ему выходной вектор. Это устройство предназначено для вычисления специфической функции. То, какую именно функцию оно вычисляет, зависит от глобальной конфигурации синаптической весовой структуры.

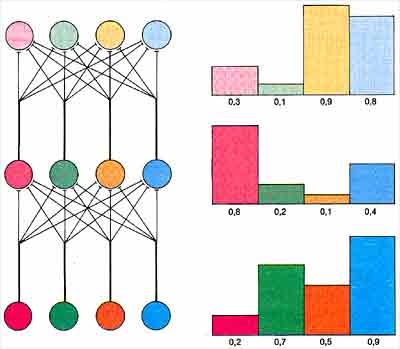
НЕЙРОННЫЕ СЕТИ моделируют главное свойство микроструктуры мозга. В этой трехслойной сети входные нейроны (слева внизу) обрабатывают конфигурацию активирующих сигналов {справа внизу) и передают их по взвешенным связям скрытому слою. Элементы скрытого слоя суммируют свои многочисленные входы, образуя новую конфигурацию сигналов. Она передается внешнему слою, выполняющему дальнейшие преобразования. В целом сеть преобразует любой входной набор сигналов в соответствующий выход, в зависимости от расположения и сравнительной силы связей между нейронами.

Существуют разнообразные процедуры для подбора весов, благодаря которым можно сделать сеть, способную вычислить почти любую функцию (т. е. любое преобразование между векторами). Фактически в сети можно реализовать функцию, которую даже нельзя сформулировать, достаточно лишь дать ей набор примеров, показывающих, какие лары входа и выхода мы хотели бы иметь. Этот процесс, называемый «обучением сети», осуществляется путем последовательного подбора весов, присваиваемых связям, который продолжается до тех пор, пока сеть не начнет выполнять желаемые преобразования с входом, чтобы получить нужный выход.

Хотя эта модель сети чрезвычайно упрощает структуру мозга, она все же иллюстрирует несколько важных аспектов. Во-первых, параллельная архитектура обеспечивает колоссальное преимущество в быстродействии по сравнению с традиционным компьютером, поскольку многочисленные синапсы на каждом уровне выполняют множество мелких вычислительных операций одновременно, вместо того чтобы действовать в очень трудоемком последовательном режиме. Это преимущество становится все более значительным, по мере того как возрастает количество нейронов на каждом уровне. Поразительно, но скорость обработки информации, совершенно не зависит ни от числа элементов, участвующих в процессе на каждом уровне, ни от сложности функции, которую они вычисляют. Каждый уровень может иметь четыре элемента или сотню миллионов; конфигурация синаптических весов может вычислять простые одноразрядные суммы или решать дифференциальные уравнения второго порядка. Это не имеет значения. Время вычислений будет абсолютно одним и тем же.

Во-вторых, параллельный характер системы делает ее нечувствительной к мелким ошибкам и придает ей функциональную устойчивость; потеря нескольких связей, даже заметного их количества, оказывает пренебрежимо малое влияние на общий ход преобразования, выполняемого оставшейся частью сети.

В-третьих, параллельная система запоминает большое количество информации в распределенном виде, при этом обеспечивается доступ к любому фрагменту этой информации за время, измеряющееся несколькими миллисекундами. Информация хранится в виде определенных конфигураций весов отдельных синаптических связей, сформировавшихся в процессе предшествовавшего обучения. Нужная информация «высвобождается» по мере того, как входной вектор проходит через (и преобразуется) эту конфигурацию связей.

Параллельная обработка данных не является идеальным средством для всех видов вычислений. При решении задач с небольшим входным вектором, но требующих многих миллионов быстро повторяющихся рекурсивных вычислений, мозг оказывается совершенно беспомощным, в то время как классические МС-машины демонстрируют свои самые лучшие возможности. Это очень большой и важный класс вычислений, так что классические машины будут всегда нужны и даже необходимы. Однако существует не менее широкий класс вычислений, для которых архитектура мозга представляет собой наилучшее техническое решение. Это главным образом те вычисления, с которыми обычно сталкиваются живые организмы: распознавание контуров хищника в «шумной» среде; мгновенное вспоминание правильной реакции на его пристальный взгляд, способ бегства при его приближении или защиты при его нападении; проведение различий между съедобными и несъедобными вещами, между половыми партнерами и другими животными; выбор поведения в сложной и постоянно изменяющейся физической или социальной среде; и т. д.

Наконец, очень важно заметить, что описанная параллельная система не манипулирует символами в соответствии со структурными правилами. Скорее манипулирование символами является лишь одним из многих других «интеллектуальных» навыков, которым сеть может научиться или не научиться. Управляемое правилами манипулирование символами не является основным способом функционирования сети. Рассуждение Сирла направлено против управляемых правилами МС-машин; системы преобразования векторов того типа, который мы описали, таким образом, выпадают из сферы применимости его аргумента с китайской комнатой, даже если бы он был состоятелен, в чем мы имеем другие, независимые причины сомневаться.

Сирлу известно о параллельных процессорах, но, по его мнению, они будут также лишены реального семантического содержания. Чтобы проиллюстрировать их неизбежную неполноценность в этом отношении, он описывает второй мысленный эксперимент, на сей раз с китайским спортивным залом, который наполнен людьми, организованным в параллельную сеть. Дальнейший ход его рассуждений аналогичен рассуждениям в случае с китайской комнатой.

На наш взгляд, этот второй пример не так удачен и убедителен, как первый. Прежде всего то обстоятельство, что ни один элемент в системе не понимает китайского языка, не играет никакой роли, потому что то же самое справедливо и по отношению к нервной системе человека: ни один нейрон моего мозга не понимает английского языка, хотя мозг как целое понимает. Далее Сирл не упоминает о том, что его модель (по одному человеку на каждый нейрон плюс по быстроногому мальчишке на каждую синаптическую связь) потребовала бы по крайней мере 10¹⁴ человек, так как человеческий мозг содержит 10¹¹ нейронов, каждый из которых имеет в среднем 10³ связей. Таким образом, его система потребует населения 10 000 миров, таких как наша Земля. Очевидно, что спортивный зал далеко не в состоянии вместить более или менее адекватную модель.

С другой стороны, если такую систему все же удалось бы собрать, в соответствующих космических масштабах, со всеми точно смоделированными связями, у нас получился бы огромный, медленный, странной конструкции, но все же функционирующий мозг. В этом случае, конечно, естественно ожидать, что при правильном входе он будет мыслить, а не наоборот, что он на это не способен. Нельзя гарантировать, что работа такой системы будет представлять собой настоящее мышление, поскольку теория векторной обработки может неадекватно отражать работу мозга. Но точно так же у нас нет никакой априорной гарантии, что она не будет мыслить. Сирл еще раз ошибочно отождествляет сегодняшние пределы своего собственного (или читательского) воображения с пределами объективной реальности.

МОЗГ является своеобразным компьютером, хотя большинство его свойств пока остается непознанным. Охарактеризовать мозг как компьютер далеко не просто, и такие попытки не следует считать излишней вольностью. Мозг дейтствительно вычисляет функции, но не такие, как в прикладных задачах, решаемых классическим искусственным интеллектом. Когда мы говорим о машине как о компьютере, мы не имеем в виду последовательный цифровой компьютер, который нужно запрограммировать и которому свойственно четкое разделение на программную часть и аппаратную; мы не имеем также в виду, что этот компьютер манипулирует символами или следует определенным правилам. Мозг — это компьютер принципиально другого вида.

Каким образом мозг улавливает смысловое содержание информации, пока не известно, однако ясно, что проблема эта выходит далеко за рамки лингвистики и не ограничивается человеком как видом. Маленькая кучка свежей земли означает, как для человека, так и для кайота, что где-то поблизости находится суслик; эхо с определенными спектральными характеристиками означает для летучей мыши присутствие мотылька. Чтобы разработать теорию формирования смыслового содержания, мы должны больше знать о том, как нейроны кодируют и преобразуют сенсорные сигналы, о нейронной основе памяти, об обучении и эмоциях и о связи между этими факторами и моторной системой. Основанная на нейрофизиологии теория понимания смысла может потребовать даже наших интуитивных представлений, которые сейчас кажутся нам такими незыблемыми и которыми так свободно пользуется Сирл в своих рассуждениях. Подобные пересмотры — не редкость в истории науки.

Способна ли наука создать искусственный интеллект, воспользовавшись тем, что известно о нервной системе? Мы не видим на этом пути принципиальных препятствий. Сирл будто бы соглашается, но с оговоркой: «Любая другая система, способная порождать разум, должна обладать каузальными свойствами (по крайне мере), эквивалентными соответствующим свойствам мозга». В завершение статьи мы и рассмотрим это утверждение. Полагаем, что Сирл не утверждает, будто успешная система искусственного интеллекта должна непременно обладать всеми каузальными свойствами мозга, такими как способность чувствовать запах гниющего, способность быть носителем вирусов, способность окрашиваться в желтый цвет под действием пероксидазы хрена обыкновенного и т. д. Требовать полного соответствия будет все равно, что требовать от искусственного летательного аппарата способности нести яйца.

Вероятно, он имел в виду лишь требование, чтобы искусственный разум обладал всеми каузальными свойствами, относящимися, как он выразился, к сознательному разуму. Однако какими именно? И вот мы опять возвращаемся к спору о том, что относится к сознательному разуму, а что не относится. Здесь как раз самое место поспорить, однако истину в данном случае следует выяснять эмпирическим путем — попробовать и посмотреть, что получится. Поскольку нам так мало известно о том, в чем именно состоит процесс мышления и семантика, то всякая уверенность по поводу того, какие свойства здесь существенны, была бы преждевременной. Сирл несколько раз намекает, что каждый уровень, включая биохимический, должен быть представлен в любой машине, претендующей на искусственный интеллект. Очевидно, это слишком сильное требование. Искусственный мозг может и не пользуясь биохимическими механизмами, достичь того же эффекта.

Эта возможность была продемонстрирована в исследованиях К.Мида в Калифорнийском технологическом институте. Мид и его коллеги воспользовались аналоговыми микроэлектронными устройствами для создания искусственной сетчатки и искусственной улитки уха. (У животных сетчатка и улитка не являются просто преобразователями: в обеих системах происходит сложная параллельная обработка данных.) Эти устройства уже не простые модели в миникомпьютере, над которым посмеивается Сирл; они представляют собой реальные элементы обработки информации, реагирующие в реальное время на реальные сигналы: свет — в случае сетчатки и звук — в случае улитки уха. Схемы устройств основаны на известных анатомических и физиологических свойствах сетчатки кошки и ушной улитки сипухи, и их выход чрезвычайно близок к известным выходам органов, которые они моделируют.

В этих микросхемах не используются никакие нейромедиаторы, следовательно, нейромедиаторы, судя по всему, не являются необходимыми для достижения желаемых результатов. Конечно, мы не можем сказать, что искусственная сетчатка видит что-то, поскольку ее выход не поступает на искусственный таламус или кору мозга и т. д. Возможно ли по программе Мида построить целый искусственный мозг, пока не известно, однако в настоящее время у нас нет свидетельств, что отсутствие в системе биохимических механизмов делает этот подход нереалистичным.

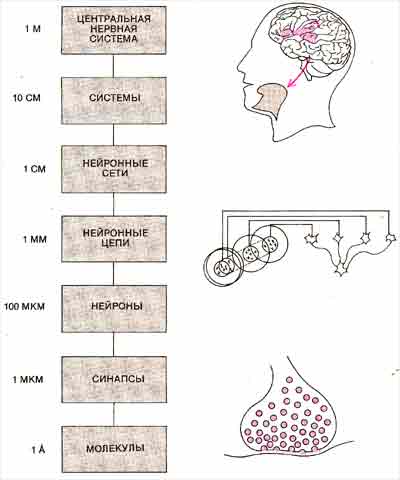
НЕРВНАЯ СИСТЕМА охватывает ыного масштабов организации, от молекул нейромедиаторов (внизу) до всего головного и спинного мозга. На промежуточных у ровнях находятся отдельные нейроны и нейронные цепи, подобные тем, что реализуют избирательность восприятия зрительных стимулов (в центре), и системы, состоящие из многих цепей, подобных тем, что обслуживают функции речи (справа вверху). Только путем исследований можно установить, насколько близко искусственная система способна воспроизводить биологические системы, обладающие разумом.

ТАК ЖЕ как и Сирл, мы отвергаем тест Тьюринга как достаточный критерий наличия сознательного разума. На одном уровне основания для этого у нас сходные: мы согласны, что очень важно, каким образом реализуется функция, определенная по входу-выходу; важно, чтобы в машине происходили правильные процессы. На другом уровне мы руководствуемся совершенно иными соображениями. Свою позицию относительно присутствия или отсутствия семантического содержания Сирл основывает на интуитивных представлениях здравого смысла. Наша точка зрения основана на конкретных неудачах классических МС-машин и конкретных достоинствах машин, архитектура которых ближе к устройству мозга. Сопоставление этих различных типов машин показывает, что одни вычислительные стратегии имеют огромное и решающее преимущество над другими в том, что касается типичных задач умственной деятельности. Эти преимущества, установленные эмпирически, не вызывают никаких сомнений. Очевидно, мозг систематически пользуется этими вычислительными преимуществами. Однако он совершенно не обязательно является единственной физической системой, способной ими воспользоваться. Идея создания искусственного интеллекта в небиологической, но существенно параллельной машине остается очень заманчивой и в достаточной мере перспективной.

Преступления, совершаемые спящими

СЕДУЕТ ли считать людей ответственными за преступления, которые они совершают во время сна? Среди психиатров наиболее распространенным является мнение, что нет, не следует, потому что, как заявил один из высококвалифицированных специалистов в этой области, «спящий разум не способен побудить намеренное действие». В письме, недавно присланном в журнал « Lancet», П. Роупер, специалист по психиатрии из Университета Макгилла, оспаривает эту точку зрения. В качестве контраргумента он выдвигает факты, связанные с поведением больной булимией (патологически сильный голод) сомнамбулы с выраженной герпетофобией (панический страх перед пресмыкающимися).

Одна жительница Монреаля могла сдерживать свою страсть к еде вовремя бодрствования. Однако в ночное время, как пишет Роупер, «она, пребывая в сонном состоянии, шла к холодильнику и съедала что-нибудь из того, что там имелось, — сырое мясо, масло, сырые овощи. Если бы больная вышла из сонного состояния и осознала свои действия, она осудила бы свой поступок и вернулась в постель, но, как правило, она не осознавала своих действий во время ночных прогулок до тех пор, пока не наступало утро, когда вдруг обнаруживала развернутые продукты, остатки пищи и общий беспорядок на кухне».

В процессе обследования психики этой женщины Роупер установил, что она также испытывала сильный страх перед змеями (герпетофобия). Действительно, она приходила в ужас даже при виде игрушечной змеи одного из двух ее детей. Роупер решил противопоставить ее герпетофобию булимии и попросил мужа пациентки, чтобы он каждый вечер перед сном клал игрушечную змею на стол у холодильника.

Эксперимент удался. В течение следующих двух с половиной лет женщина совершила всего шесть ночных «налетов» на холодильник. Во всех этих случаях, как позже призналась пациентка Роуперу, она заранее, перед тем как лечь спать, замечала, что муж забывал положить змею; она не считала нужным напоминать ему о его обязанностях.

В эти ночи, указывает Руопер, спящую женщину не оставляло знание, полученное ею во время бодрствования, и она руководствовалась им для удовлетворения своего неотступного желания поесть. Нет сомнения, говорит он, что лунатики — это не бездумные «автоматы», как их представляют некоторые психиатры. «Концепция о том, что «спящий разум не способен побудить намеренное действие», — приходит к выводу Роупер, — может, следовательно, быть ошибочной, и врачи должны учитывать это, когда дают свои заключения в связи с расследованием преступлений, совершаемых в состоянии сомнамбулизма».

Такие случаи не часты, но все же имеют место, указывает Роупер. Он отмечает, что несколько лет назад, например один житель пригорода Торонто утверждал, что он находился в спящем состоянии, когда на протяжении 10 миль вел автомобиль, направляясь к теще, а приехав ударил ее и нанес смертельную рану ножом. Суд оправдал его.

Продлить прошлое

ВРЕМЯ целаканта, похоже, в конце концов скоро иссякнет — таково мнение группы ихтиологов, объединившихся в Совет по охране целаканта. Хотя эта крупная (до 1,5 м в длину) рыба не съедобна и живет на глубине более 70 м, из-за высокой цены, которую дают сейчас за неё, а также появления усовершенствованных рыболовных снастей рыбаки целенаправленно охотятся за целакантом.

Целакант считается близкородственным общему предку всех наземных животных. Ранее полагали, что он вымер около 70 млн. лет назад. Но в 1938 г. был случайно выловлен один экземпляр. Это живое ископаемое встречается только в Индийском океане вокруг Коморских островов. Нынешняя его численность неизвестна; по мнению М. Брутона из Смитовского института ихтиологии в Грей-амстауне (ЮАР), на сегодняшний день существует только несколько сотен особей.

Беспокойство о судьбе этой скорее всего неустойчивой популяции побудило вышеупомянутый Совет осудить амбициозный план, выдвинутый сотрудниками Аквариума Тоба в Японии: они намерены содержать пару целакантов в неволе. Члены Совета опасаются, что это разожжет конкуренцию в мировом масштабе. Директор проекта, предполагающего содержание целакантов в неволе, X. Накамура заявил, что если этих рыб удастся поймать и сохранить в живых, два экземпляра будут переправлены в Японию для изучения, чтобы подготовить их к разведению в неволе. Исследователи, вошедшие в Совет, высказывали сомнение в осуществимости этого плана, подчеркивая, что целакант может жить вне воды только несколько часов (вероятно, из-за чувствительности к перепадам температуры и давления). На это Накамура отвечал, что в Аквариуме Тоба разработана особая ловушка с системой жизнеобеспечения, создающей необходимые для целаканта условия. Однако конструкцию этой ловушки он не раскрывает.

Совет не разделяет уверенности Накамуры. Коль скоро предпринимается действительно научная работа, не следует секретничать. Бретон и его коллеги испытывают сомнения еще и по другому поводу. Поскольку целакант достигает зрелости в 10-15 лет, разводить его в неволе вряд ли будет эффективно. Притом состояние этого вида в природе сейчас таково, что нельзя рисковать жизнью даже пары особей, подвергая их транспортировке через полмира. Ихтиологам — членам Совета — более импонирует интенсивная научно-исследовательская работа и сохранение известных природных популяций.

В приложении к Конвенции о международной торговле видами фауны и флоры дикой природы, находящихся под угрозой исчезновения, целакант недавно занесен в категорию видов, подлежащих охране в первую очередь. Однако Накамура не считает, что целакант следует расценивать как редкий вид. По его словам, обвинения со стороны Совета — это не что иное, как плод раздражительности на почве «научного снобизма».

В МИРЕ НАУКИ. (Scientific American. Издание на русском языке) • 1988 No4. стр. 81-85

ЗАНИМАТЕЛЬНЫЙ КОМПЬЮТЕР

---

Моделирование эволюции в мире биоморфов

А.К.Дьюдни

ЕСЛИ живые существа уподобить часовым механизмам, то создавший их часовой мастер, по мнению Р.Докинза, биолога из Оксфорда, автора книги «Эгоистичный ген» (The Selfish Gene), должен быть слепым. В конце концов эволюцией управляют слепые физические силы. Докинз присоединился к полемике между креационистами и эволюционистами, поддерживая последних, о чем свидетельствует написанная им недавно другая книга - «Слепой часовой мастер» (The Blind Watchmaker). Чтобы проиллюстрировать одно из главных положений своей книги, Докинз написал компьютерную программу, которая позволяет пользователю моделировать эволюционный процесс, придумывая и графически изображая свои собственные формы жизни, абстрактные организмы, которые Докинз называет биоморфами.

Программа, которую мы так и назовем WATCHMAKER (часовой мастер), демонстрирует ошибочность довода, часто выдвигаемого критиками теории эволюции. Каким образом нечто такое сложное, как «машина жизни», может возникнуть просто в результате стечения случайных событий? На первый взгляд кажется, что это действительно невероятно. Интуитивно мы чувствуем, что здесь не обошлось без «часового мастера», как говорил У.Пэйли, английский теолог, живший в XVIII в. Доказывая, что у всех форм жизни должен быть Создатель, Пэйли рассуждал следуюшим образом. Если, идя по полю, мы наткнемся на камень, то можно, конечно, подумать, что он лежал там вечно. «Однако предположим, - писал Пэйли, - что я нашел на земле часы и захотел узнать, как они здесь оказались. Едва ли я удовлетворюсь тем же ответом, что и в предыдущем случае... Часы, должно быть, имели своего творца».

Пэйли умер еще до того, как родился Чарлз Дарвин, однако современные креационисты соглашаются с аргументом Пэйли. При каком стечении случайных событий могли появиться часы на поле, о котором говорит Пэйли? Ошибочность этого аргумента заключается в неявном предположении, что случайные события, которые привели к появлению часов (или их творца), происходили более или менее одновременно. Здесь не принимаются в расчет эффекты кумулятивных, т. е. накапливающихся изменений. Программа WATCHMAKER как раз и показывает на примере вычислительных процессов, сколь значительными могут быть кумулятивные изменения. Правда, творения этой программы - не живые организмы, а лишь биоморфы: статические формы, напоминающие живых существ.

Процесс начинается с очень простого образования в центре экрана, который делится на большие клетки:

Генетические вариации нейтрального дерева

Предположим, к примеру, что центральная клетка содержит маленькое дерево с несколькими ветвями. Программа WATCHMAKER порождает деревья - вариации исходного, которые заполняют соседние клетки на экране. У одних деревьев становится больше веток, у других меньше, одни становятся выше, другие ниже. Характер изменений, которым могут подвергаться деревья, определяется некоторым набором генов. Но об этом мы поговорим несколько позже. Все производные деревья рассматриваются как потомки центрального дерева. Они представляют собой те видоизменения, которые возможны в популяции на данный момент.

Программа WATCHMAKER выполняется на персональном компьютере «Макинтош». Поэтому эволюционный процесс управляется «мышью» - устройством ввода, которое пользователь перемещает рукой по контактной площадке. Движение мыши сопровождается таким же движением маленького темного квадратика - указателя на экране компьютера. В ходе работы программы WATCHMAKER пользователь выбирает, какое из изображенных на экране деревьев должно дать потомство в следующем поколении. Для этого нужно загнать указатель, управляемый мышью, в один из квадратов, в котором находится выбранное дерево. У мыши есть кнопка, на которую нужно нажать, когда указатель уже находится в выбранной клетке; в этом случае все последующие деревья будут потомками выбранного. Оно перемещается в центральный квадрат. Теперь цикл отбора повторяется. Такая селекционная последовательность порождает филогенетическую линию деревьев, представители которой в каждом поколении несколько отличаются от родителя. Однако медленное накопление незначительных изменений может привести к удивительным результатам.

Докинз пишет, что, собираясь в первый раз запустить программу WATCHMAKER, он «надеялся увидеть плакучие ивы, ливанские кедры, ломбардийские тополя, водоросли, и может быть, оленьи рога. Но ни моя интуиция биолога, ни двадцатилетний опыт программирования компьютеров, ни самые необузданные полеты моей фантазии не подготовили меня к тому, что я увидел на экране в действительности. Я уже не помню, глядя на какой элемент последовательности, я начал впервые подозревать, что... может получиться нечто вроде насекомого... Все меньше веря своим глазам, я наблюдал, как сходство с насекомым становится все более отчетливым». И вот, наконец, под триумфальные звуки фанфар на экране появились насекомоподобные существа:

Насекомоподобные биоморфы, порожденные программой WATCHMAKER

Докинз плохо спал в ту ночь, перед его глазами роились насекомые.

Так появилась первая из тех форм, для которых позже Докинз придумал общее название биоморфы. На самом деле все формы, порождаемые программой, представляли собой деревья. Причудливо изгибающиеся ветви могут придать этим деревьям формы, в которых мы узнаем не только тело, крылья и ножки насекомых, но и мириады других биоморфов, включая древовидных лягушек, летучих мышей и даже орхидеи. Могут появиться и такие технические формы, как лампочки и лабораторные весы:

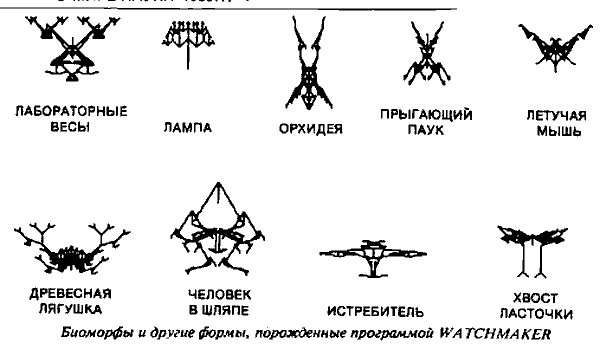
Каким же образом программа «исполняет вариации на заданную тему»? Как я уже говорил, форма каждого дерева, порождаемого программой, определяется генами. Всего их 16. Роль некоторых генов объяснить просто. Эффект других заранее предсказать невозможно, потому что их роль зависит от взаимодействия с третьими. Несколько генов определяют количество ветвей и общие размеры дерева. Из генов второго типа три гена в определенных сочетаниях влияют на горизонтальную протяженность ветвей, в то время как пять других совместно определяют их вертикальную протяженность.

Мир Докинза представляет собой 16-мерное пространство, населенное всевозможными вариантами биоморфов. В конце концов каждое существо полностью определяется набором из 16 чисел, представляющих его генетическую наследственность. Эти числа можно считать значениями координат, и тогда каждый биоморф становится просто точкой в пространстве, которое Докинз называет миром биоморфов. Программа WATCHMAKER представляет собой отличное средство, при помощи которого можно исследовать этот мир.

Программа Докинза слишком длинна и сложна, и я не смогу ее здесь описать прежде всего потому, что в ней осуществляется выбор большого количества различных режимов и параметров, и каждую процедуру выбора можно считать отдельной программой. Например, в программе можно выбрать режим конструирования. Пользователь знакомится с комментарием, прилагаемым к программе, чтобы научиться непосредственно манипулировать генами, с целью получить те или иные конкретные биоморфы. Среди других режимов есть и так называемая «история ископаемых останков». В этом режиме эволюционные ветви хранятся в виде отложений различных исторических эпох. Есть также режим «в поисках чудовища», в котором происходит случайный отбор потомства в каждом поколении. Этот процесс продолжается до тех пор, пока не появится какая-нибудь интересная форма, может быть даже чудовище.

Вот здесь креационист, наверное, воскликнет: «Обман!» - И не без оснований. Ведь это, по существу, искусственный отбор выживающих вариантов, совершаемый человеком. Другими словами, это не естественный отбор, а направленная селекция. Дарвин говорил об успешной деятельности селекционеров, чтобы подкрепить свой тезис о существовании изменчивости в популяциях. Конечно, эта деятельность не доказывает существования естественного отбора. Аргументы в пользу последнего Дарвин черпал из многих источников, в том числе он их находил и в истории ископаемых останков. Цель, преследуемая Докинзом, тем не менее была достигнута. Эффекты накапливающихся изменений могут быть весьма впечатляющими. Они были бы еще более впечатляющими, если на обвинение в обмане можно было ответить более непосредственным образом. Нельзя ли, скажем, сделать так, что бы процедура отбора в программе не направлялась человеком и даже не была случайным процессом, а определялась в той или иной форме требованиями окружающей среды? Могла бы эволюция быть результатом конкурентного взаимодействия между различными видами?

Докинз сформулировал следующую задачу для программистов: «Биоморфы должны взаимодействовать в компьютере, который моделировал бы враждебную среду. Какие-то детали формы организмов должны определять, выживут они или погибнут в данной среде». Он указывает, далее, что уязвимость организмов должна следовать из самой модели, а не быть заранее «встроенной» программистом. Число генов можно варьировать. Докинз считает, что если кто-нибудь и справится с задачей, то это будут программисты из «числа тех, кто сочиняет всем знакомые видеоигры». Должен сказать, что я в этом сомневаюсь.

Хотя сам я, наверное, не справлюсь с задачей Докинза, я все же могу проиллюстрировать в общих чертах модель, которую он имел в виду. В конце концов можно придумать два каких-нибудь взаимодействующих вида, которые постепенно изменяются в результате взаимодействия. Однако уязвимость видов я как «часовой мастер-любитель» встроил в них заранее. Возможно, описанный ниже пример вдохновит кого-нибудь из читателей, и он превзойдет мою скромную попытку, создав настоящую эволюционную (если не сказать революционную) программу.

Рассмотрим организмы, изображенные на рисунке внизу. Назовем их шипофитом и гнутозавром. Гнутозавр не может жить без сочных листьев, растущих на верхушке шипофита. К сожалению, у основания шипофит окружен ошейником из колючих ядовитых шипов. Однако гнутозавр, как говорит само его имя, имеет в своем теле изгиб, позволяющий ему избегать смертельных уколов колючек шипофита, когда он пытается достать сочные листья последнего.

Взаимозависимая эволюция шипофита и гнутозавра

Это, как говорится, хорошо. Плохо же то, что гнутозавр ужасно негибкий. Его тело всегда изогнуто под углом 90°. Более того, ни шея, ни тело его не гнутся. Поэтому гнутозавр осужден на то, чтобы есть листья лишь на определенном уровне, конечно, при условии, что его шея окажется достаточно длинной, чтобы достать их.

Само собой разумеется, что обе популяции подвержены случайным вариациям в своем генетическом коде. Гнутозавры могут быть различной высоты (измеряемой по высоте плеч) и могут иметь шеи разной длины. Колючки шипофита все одинаковой длины у одного и того же растения, но их длина может быть неодинаковой у разных растений. Высота шипофита также подвержена небольшим случайным изменениям.

Чтобы управлять формой каждого из этих биоморфов, им достаточно иметь по два гена. У гнутозавра один ген ответствен за высоту, другой за длину шеи. У шипофита также два гена, один задает высоту и один длину шипов. При определенных условиях, указанных в программе, которую я назвал ESCAPEMENT эволюция этих двух форм жизни может быть взаимозависимой. В эволюционной перспективе изменения своих генов шипофит «стремится» избавиться от гнутозавра (отсюда название программы: escapement, что в переводе означает «избавление»), видоизменяясь так, чтобы последнему было все труднее добывать его листья.

Программа ESCAPEMENT поочередно предоставляет возможность обоим биоморфам изменять свою форму. Например, шипофит может стать несколько выше или ниже, а его шипы - длиннее или короче. Высота тела и длина шеи гнутозавра также могут меняться в ту и другую сторону. Поскольку для обоих биоморфов существуют абсолютные верхние пределы размера, бесконечная «гонка вооружений» невозможна. Например, сумма длины шипов и высоты ствола шипофита не может превысить некоторого предельного значения, которое я назову smax. Аналогичным образом длина гнутозавра, измеряемая от его головы до кончиков пальцев на ногах, не превышает предельного значения bmax. Чтобы сделать модель интереснее, я решил, что bmax будет больше smax.

Каким образом программа ESCAPEMENT решает, какой из потомков каждого биоморфа выживет? Критерий заключается в величине, называемой дистанцией кормления. Она измеряет расстояние между головой гнутозавра и ароматными листьями шипофита. Предположим гнутозавр имеет рост w, а длина его шеи равна х. Если высота ствола шипофита равна у, а длина его колючек z, то дистанция кормления выражается обычной формулой евклидова расстояния: квадратным корнем из величины (z - х)² + (у - w)². Если z оказывается меньше х, формула изменяется. В этом случае гнутозавр может стоять сколь угодно близко к шипофиту, и рассматривается только второй член формулы.

Неудивительно, что шипофит стремится эволюционировать так, чтобы максимально увеличить дистанцию кормления. Задача гнутозавра, наоборот, заключается в том, чтобы сделать это расстояние минимальным. Каждый биоморф, когда до него доходит очередь, порождает двух отпрысков. Например, если высота шипофита в данном поколении равна у, то в следующем она может стать равной у - 1 или у + 1. Длина шипов может либо увеличиться от z до z + 1, либо уменьшиться до z - 1.

В каждом случае выбор осуществляется случайным образом. Аналогично возникают два видоизмененных потомка у гнутозавра. Вместе с двумя видоизмененными потомками родительский биоморф сохраняется для последующего оценивания перед лицом своего биологического противника. Критерием и в этом случае является дистанция кормления. Например, тот из трех шипофитов, которому удается держать «живущего» в данный момент гнутозавра на наибольшей дистанции, отбирается, так сказать, в квазиестественном процессе и сохраняется для следующего раунда эволюции. Теперь наступает очередь гнутозавра. Он сам и его два видоизмененных потомка проверяются на выживание в среде с новой моделью шипофита. Тот, у которого дистанция кормления окажется минимальной, будет родителем нового поколения.

Было бы замечательно, если бы программа ESCAPEMENT имела графические возможности, позволяющие ей изображать шипофитов и гнуто-завров, представителей двух древних и знаменитых биоморфов, так, как это сумел сделать наш художник. Однако это выше моих возможностей. Я остановил свой выбор на простейших диаграммах, одна из которых приведена на самом рисунке. Здесь нет практически ничего, кроме представления основных переменных в виде прямолинейных отрезков. Читатели, которые не пожелают возиться даже с такими простейшими изображениями, могут удовлетвориться тем, чтобы программа просто распечатывала значения четырех переменных в конце каждого раунда.

Программа ESCAPEMENT построена в виде единого цикла, в теле которого оба биоморфа изменяются, оцениваются и демонстрируются:

input bmах, smax
input w, х, у, т.
input gen
for i - 1 to gen

создать потомков шипофита
оценить шипофитов
создать потомство гнутозавра
оценить гнутозавров
показать победителей

Пользователь, конечно, должен ввести исходные значения шести основных переменных от руки, а также задать значение величины gen, число поколений, или витков эволюции. Затем выполняются итерации в двух внутренних подциклах размножения биоморфов, их оценивания и показа. Биоморф воспроизводится путем выбора двух случайных чисел, определяющих, увеличится или уменьшится значение каждого гена. Например, алгоритм, с помощью которого порождаются два видоизмененных гнутозавра, получает мутации а и Ь соответственно для генов w и х следующим образом:

r - random
if r< 0,5 then a = w - 1
else a = w + 1
s = random
if s < 0,5 then b = x - 1
else b = x + 1

Теперь программа располагает тремя гнутозаврами. Их генетические наборы могут быть представлены в виде трех пар чисел: [w, х], [а, х], [w, b]. Который из них является наилучшим? Программа ESCAPEMENT оценивает эти три модели, подсчитывая для них соответствующие дистанции, на которых гнутозавры могут добыть себе корм с каждой текущей модели шипофита. Обозначив дистанции dl, d2 и d3, их можно вычислить по существу с помощью одной и той же формулы. Вот, например, как программа вычисляет второе расстояние, d2, между гнутозавром [а, х] и шипофитом [ у, z]:

if x < z then d2 = (z - x}² + (у - а)²
else d2 = (у - а)²

В каждом случае применяется формула евклидова расстояния, в которую подставляются соответствующие координаты головы животного и листа растения. Когда все три расстояния вычислены, наименьшее из них определяется путем последовательных сравнений:

if d2 <= dl and d2 <= d3
then w = a

if d3 <= dl and d3 <= d2
then x = Ь

Если ни одно из двух пар неравенств не удовлетворяется, то родитель сохраняет превосходство над своими потомками. Поэтому гены х и w остаются прежними. Аналогичным образом программа оценивает шипофитов с той лишь разницей, что по отношению к растениям в качестве критерия способности выжить берется не минимум, а максимум расстояния.

Пока мы еще ничего не сказали о пределах роста, о чем упоминалось выше. Каким образом программа ESCAPEMENT препятствует неумеренному росту каждого из биоморфов? Простейший способ заключается в том, чтобы наказывать биоморфа-переростка при вычислении расстояния. Например, если видоизмененный гнутозавр [а, х] окажется слишком большим, то сумма а + х превысит значение bmах. В этом случае к подсчитанному расстоянию можно прибавить, скажем, 1000, чтобы этот мутант не оказался победителем. Шипофиты-переростки могут наказываться, наоборот, путем вычитания 1000 из вычисленного для них расстояния. Аналогичным образом оба биоморфа должны наказываться в том случае, если любая из четырех переменных окажется отрицательной.

Победители по результатам оценки демонстрируются на экране дисплея с помощью простых графических команд, обычно имеющихся в большинстве языков программирования. Эту часть программы мы оставляем воображению читателей.

Что же происходит с биоморфами при выполнении программы ESCAPEMENT? В какой-то степени это зависит от исходных значений четырех генов и двух предельных размеров, вводимых перед началом выполнения программы. Значения переменных могут также зависеть от размеров экрана. Пусть, например, smax будет равно 100, а bmах 110. Тогда мы будем наблюдать интересное явление. Выберем исходные значения для четырех генов произвольно в диапазоне от 0 до 50. Можно, например, начать с хорошо сбалансированных биоморфов, либо высоких и худых, либо низких и толстых. По мере того как одно поколение сменяет другое, мы становимся свидетелями гонки. Гнутозавр может «преследовать» шипофита, производя все более высоких и худых потомков, и, в конце концов, обогнав в росте растение, преградить ему путь вверх. Тогда шипофит может попытаться «убежать» вниз, все более широко расставляя свои ядовитые колючки. Гнутозавр в свою очередь тоже будет становиться более приземистым, а его шея начнет удлиняться. Таким образом, при выполнении простого требования, чтобы значение bmах превосходило smax, будет всегда возникать кажущаяся бесконечной последовательность из побегов и погони. Читатели, обладающие хорошим воображением, возможно, смогут представить себе, какими будут результаты в противном случае.

Разумеется, когда мы говорим о побеге и погоне, мы имеем в виду не отдельных биоморфов, а «историю ископаемых останков». Наверное, палеонтолог, исследующий всю последовательность слоев отложений с ископаемыми шипофитами и гнутозаврами, будет немало удивлен, как оба вида меняли свои размеры со временем подобно раскачивающемуся маятнику.

Докинз предлагает читателям его книги самим заняться разработкой экспериментальных программ, которые позволяют исследовать эволюционные процессы. Эти программы могут быть либо усовершенствованными версиями ESCAPEMENT, либо представлять собой значительно более глубокие разработки.

Споры между креационистами и эволюционистами не утихают, но, может быть, и те и другие одинаково далеки от истины? Забавная мысль: представим себе Творца, способного создавать пути эволюции и с улыбкой наблюдающего за тем, как ломают копья сторонники двух противоположных концепций.

ИГРА под названием ГВУ (Гарантированное взаимное уничтожение) была темой нашей статьи в декабрьском номере журнала за прошлый год. Придуманная в 1985 г. Т. Хомер-Диксоном и К. Оливо из Массачусетского технологического института, игра моделирует стратегию двух сверхдержав, балансирующих на грани между войной и миром. Были проведены эксперименты, в которых студенты МТИ, сидя за клавиатурами компьютеров, играли роль руководителей государств. Какой стратегии придерживаться? Воздерживаться от нападения и получать таким образом относительно скромную прибавку к очковому балансу или начать военные действия в надежде значительно изменить этот баланс в свою пользу? По мере того как развиваются события, потенциальный выигрыш стороны, принявшей решение атаковать первой, резко возрастает.

Несмотря на тот факт, что перед частью студентов была поставлена цель достичь наибольшего количества очков, чему лучше всего способствует мирная политика, многие из них не стали ее придерживаться. В их числе оказался и Д.Фармер из Миссисога (Канада, провинция Онтарио), попытавшийся проанализировать сходную игру, применив принципы теории игр. В теории рассматриваются лишь так называемые матрицы игры в отрыве от последующих ходов. Теория также требует максимально увеличивать счет, сводя к минимуму потери на каждом этапе игры. Чтобы воспользоваться теорией, Фармер нашел способ генерировать новые игровые матрицы, отражающие последующий ход игры. В своем письме Фармер рассмотрел пример с пятью центральными матрицами игры ГВУ. По мнению Фармера, наиболее благоприятный момент для нападения возникает на втором этапе. Однако он заключает: «Перед лицом все возрастающей угрозы опустошительного первого удара, чтобы следовать мирной стратегии, нужно руководствоваться соображениями, выходящими за пределы теории игр. С другой стороны, если негативные последствия будущих военных сценариев сделать менее негативными, то даже теория отдаст предпочтение мирной стратегии. Переговоры о разоружении способствуют уменьшению угрозы войны в будущем, модифицируя таким образом баланс очков в положительном направлении».

В последних стадиях игры ГВУ возникает ситуация, известная под названием «Дилеммы арестованного»: вознаграждение за признание (соответствующее за нападение в ГВУ) становится настолько большим, что возникает соблазн «нажать кнопку». И все же турнир по игре «Дилемма арестованного», проведенный несколько лет назад в Мичиганском университете, показал, что наилучшей стратегией в игре была стратегия «око за око», т. е. пока ваш оппонент воздерживается, вам тоже лучше воздерживаться. Теперь студенты (и вообще все желающие) могут проводить свои собственные турниры по игре «Дилемма арестованного». Уже существует программное обеспечение игры для компьютера Макинтош, а вскоре будут готовы и программы для персонального компьютера фирмы IBM и совместимых с ним компьютеров. Авторы этих программ - Л. Беркхолдер и К. Уолтон из Университета Карнеги - Меллона.

В МИРЕ НАУКИ. (Scientific American. Издание на русском языке) • 1990 No2. стр. 82-86

ЗАНИМАТЕЛЬНЫЙ КОМПЬЮТЕР

---

О разуме, машинах и метафизике

А.К.Дьюдни

«Подчиняется ли разум физическим законам?
Да и что такое физические законы?»
РОДЖЕР ПЕНРОУЗ «Новый ум императора»

ЧЕЛОВЕЧЕСКИЙ разум превосходит системы искусственного интеллекта, потому что использует физические законы на квантовомеханическом уровне. К такому не бесспорному утверждению склоняется в своей новой книге Роджер Пенроуз, известный ученый, работающий в области математической физики. Хотя (как признает Пенроуз) это утверждение в настоящее время не может быть строго доказано, некоторые интригующие аргументы, содержащиеся в его книге «Новый ум императора», дают достаточно серьезные основания усомниться в справедливости философских положений, которые лежат в основе искусственного интеллекта.

Ниже мы рассмотрим аргументы Пенроуза, но поскольку в данной рубрике мы пользуемся своим компасом, совершая плавание по неизведанным морям, я подвергну критике некоторые его выводы, а некоторые его идеи попробую развить. В частности, вопрос «Как же все-таки люди думают?» я поставлю в более широком плане и сформулирую его так: «Получат ли люди когда-нибудь достаточно знаний, чтобы ответить на такой вопрос?» Если структура Вселенной бесконечна, то люди, вероятно, никогда не смогут ответить на этот вопрос в полной мере. С другой стороны, бесконечная регрессия структуры позволяет подойти к ответу на поставленный вопрос расчетным путем.

Но прежде чем погрузиться в рассматриваемую проблему, я приглашаю читателей вместе со мной исследовать глубины «Нового ума императора». Сначала мы посетим знаменитую китайскую комнату, чтобы узнать, понимают ли «разумные» программы, что они делают. Затем нанесем короткий визит в бильярдный зал, где увидим бильярдный стол, на котором с учетом законов классической физики об упругих столкновениях могут совершаться практически любые вычисления. Перейдя в лабораторию Эрвина Шредингера, мы справимся о здоровье его кошки, чтобы проанализировать отношение между классической физикой и квантовой механикой. И наконец, достигнув пункта назначения, мы рассмотрим компьютер с бесконечным интеллектом, способный решать такие задачи, которые ни один обыкновенный конечный компьютер никогда не сможет одолеть.

Несколько лет назад внимание Пенроуза привлекла телевизионная передача, в которой сторонники искусственного интеллекта позволили себе, с его точки зрения, неосторожное заявление. Они утверждали, что компьютеры, принципиально не очень отличающиеся от существующих, через какое-то время смогут проявить себя не менее разумными, чем люди, - а может быть, и превзойти их. Пенроуз был раздражен этим заявлением. Каким образом все тонкости человеческого интеллекта, в особенности его творческие способности, могут возникнуть из алгоритма, «щелкающего» в электронном мозге компьютера? Эти невероятные утверждения заставили его заняться исследованиями, которые, в свою очередь, привели к появлению книги «Новый ум императора».

Методично изучив теорию вычислений, Пенроуз подверг критике одно из ее ключевых положений - тест Тьюринга. Многие специалисты принимают этот тест в качестве критерия, с помощью которого можно отличить разумную программу от неразумной. Тест заключается в следующем. Человек-экзаменатор печатает сообщения двум скрытым от него субъектам, одно человеку, другое компьютеру, запрограммированному так, чтобы разумно отвечать на вопросы. Если в ходе достаточно продолжительного эксперимента экзаменатор не сможет отличить ответы человека от ответов компьютера, то программа успешно проходит тест Тьюринга.

Пенроуз отмечает, что тест дает лишь косвенное свидетельство наличия разума. В конце концов, то, что иногда кажется разумным, на самом деле может оказаться пародией, точно так же, как предмет и его зеркальное отображение, которые внешне, хотя и выглядят одинаково, все же различаются во многих других аспектах. Пенроуз утверждает, что прямой метод измерения разума может потребовать значительно большего, чем простой тест Тьюринга.

Чтобы подкрепить свою аргументацию, Пенроуз прибегает к так называемой «китайской комнате», своеобразной вариации на тему теста Тьюринга, которая была предложена философом Дж. Сирле. Человек-экзаменатор стоит перед дверью в комнату, через которую могут входит и выходить лишь письменные сообщения. Экзаменатор пишет некую историю, а также ряд относящихся к ней вопросов и передает сообщение в комнату. При этом необходимо соблюдать одно необычное требование: сообщения, как входящие, так и выходящие, должны быть написаны китайскими иероглифами. Чтобы ситуация выглядела еще более необычной, человек, находящийся в комнате, выполняет программу, которая реагирует на представленную ей историю, отвечая на прилагаемые к ней вопросы. Этот человек полностью заменяет собой компьютер. Его работа была бы скучной и утомительной, но после того, как он овладевает правилами работы машины, у него уже не возникает никаких сложностей. Гарантией неведения человека-компьютера служит то, что он не знает китайского языка. Тем не менее то, что (или кто) находится в китайской комнате, кажется, прекрасно понимает рассказ и разумно отвечает на вопросы.

Этот мысленный эксперимент, по мнению Пенроуза, приводит нас к выводу, что «простой факт выполнения удачного алгоритма еще не свидетельствует о наличии какого бы то ни было понимания». Этот вывод, разумеется, справедлив по отношению к тому, кто выполняет программу, будь то человек или компьютер. В конце концов, в принципе, выполняется ли программа человеком или компьютером, не имеет значения для взаимодействия этой программы с внешним миром.

Но именно по этой причине человек в китайской комнате - это что-то вроде соломенного чучела. Никто не станет придираться к программе лишь на том основании, что выполняющая ее аппаратура ничего в ней не понимает. С еще большей строгостью можно сказать, что никому и в голову не придет критиковать поведение нейрона за то, что он не понимает смысла в тех импульсах, которые воздействуют на него и которые он сам вырабатывает. Это справедливо, независимо от того, выполняет нейрон лишь часть алгоритма или решает значительно более сложные задачи. Таким образом, любое свидетельство о наличии разума в искусственном интеллекте должно содержаться в самом алгоритме. Именно здесь Пенроуз наносит свой следующий удар.

Мир алгоритмов по существу сводится к миру вычислимых задач. По словам Пенроуза, алгоритмы представляют собой «лишь очень узкую и ограниченную часть математики». Пенроуз верит (так же, как я и многие другие математики), что математические объекты обладают своеобразной платонической реальностью. Одно из свидетельств существования таких объектов заключается в нашей полной неспособности изменить их. Они просто даны нам, как горы или океаны.

В качестве примера Пенроуз приводит множество Мандельброта. Оно не было «изобретено» Бенуа Б. Мандельбротом, известным исследователем из фирмы IBM, оно было им открыто. Подобно планете Нептун, множество существовало задолго до того, как его увидели люди и поняли его значение. Множество Мандельброта несет в себе важное сообщение тем, кто считает его созданием компьютера. Это вовсе не так. Множество Мандельброта даже невозможно вычислить! Не слышу ли я возгласов возмущения? Строго говоря, Пенроуз прав.

Множество Мандельброта, хотя оно является лишь одним из объектов платонического мира, находится довольно далеко от сферы интересов людей, которые занимаются исследованием алгоритмов. Читатели, наверное, помнят, что внутреннюю часть множества можно найти с помощью итерационного процесса: комплексное число с возводится в квадрат, затем результат, z₁, возводится в квадрат и прибавляется к с, затем второй результат, z₂ возводится в квадрат и складывается с с и т. д. Если последовательность значений z, полученных таким образом, никогда не уходит в бесконечность, то с принадлежит внутренней части множества. Однако здесь возникает трудный вопрос. Как долго следует продолжать процесс, чтобы убедиться, что последовательность остается ограниченной? По существу правильный ответ - бесконечно долго!

На практике вычисления прерываются на некотором этапе. При этом неизбежно во множество оказываются включенными несколько точек, не принадлежащих ему, поскольку для них должно пройти больше времени, прежде чем проявится неограниченность соответствующих последовательностей. Трудности, возникающие при вычислении множества Мандельброта, ничтожны в сравнении с другими ограничениями, присущими алгоритмам. Например, математика сама по себе формально считается построенной из аксиоматических систем. Предложите небольшой набор аксиом, определите одно-два правила вывода - и у вас есть математическая теория. Концептуальный алгоритм, называемый «алгоритмом британского музея», генерирует все возможные теоремы, которые доказуемы в рамках формальной системы аксиом и правил вывода. К сожалению, полученные таким образом теоремы необязательно содержат в себе все истины данной системы.

Это открытие, сделанное математиком Куртом Геделем, сокрушило надежды на то, что вся математика может быть механизирована. Пенроуз пользуется знаменитой теоремой Геделя как свидетельством, что человеческий интеллект способен превзойти возможности алгоритмического метода: «... из теоремы Геделя со всей очевидностью следует, что понятие математической истины не может быть заключено в рамки какой бы то ни было формальной схемы». Но тогда возникает вопрос: «Как может сама теорема Геделя быть результатом алгоритма?»

Я не могу дать ответа на этот вопрос, хотя мне известно, что он уже обсуждался. Возможно, что теорему Геделя можно вывести из других аксиом и правил вывода и, следовательно, ее можно получить при помощи алгоритма. Теорема может быть лишь частью нескончаемого потока метатеорем. Я был бы благодарен знающим читателям, которые помогли бы разобраться в этом вопросе.

Однако, каким бы ни было наше мнение на этот счет, «Новый ум императора» атакует претензии искусственного интеллекта на другом фронте: со стороны физики вычислений. Пенроуз склонен считать, что вычислительные процессы в значительно большей мере «чувствуют себя как дома» в ощутимом мире классической физики, нежели в непостижимом царстве квантовой механики. Современный компьютер является детерминированной системой, которая главным образом просто выполняет алгоритмы. В несколько шутливой манере Пенроуз выбирает бильярд, так часто служащий в качестве примера при изучении классических столкновений, как подходящую среду для компьютера, работающего в классическом стиле.

Если изменить конфигурацию бортиков бильярдного стола, то можно построить своеобразный компьютер, в котором бильярдные шары действовали бы в качестве носителей сигналов, а их взаимодействие играло бы роль логических операций. Бильярдный компьютер был впервые сконструирован несколько лет назад исследователями из Массачусетского технологического института Э. Фредкином и Т. Тоффоли. О простоте и эффективности бильярдного компьютера читатели могут судить сами, рассмотрев диаграмму, приведенную внизу.

На диаграмме представлено бильярдное логическое устройство. Два входных канала принимают движущиеся шары в специальную камеру, которая имеет три выходных канала. Если в камеру через один из входных каналов входит только один шар, он покинет ее либо по нижнему, либо по верхнему правому выходному каналу. Однако если в камеру одновременно входят два шара, то один из них покинет ее через выходной канал, расположенный справа внизу. Присутствие или отсутствие шара в данном выходном канале представляет результат известной логической операции, выполняемой вентилем И. На выходе шар появляется тогда и только тогда, когда один шар поступает в первый входной канал и другой шар - во второй канал.

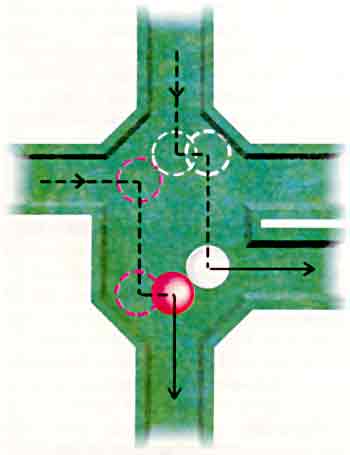
Вентиль И на бильярдных шарах

Компьютер можно построить, пользуясь вентилями только что описанного типа и еще одного типа, представляющего собой камеру, которую шар покидает по определенному каналу тогда и только тогда, когда по другому каналу не входит шар. Читателям, наверное, будет интересно сконструировать камеру такого типа, имея в виду, что полезную роль в этом устройстве могут сыграть дополнительные шары.

Нам всем нравится наблюдать за плавными, классическими движениями бильярдных шаров. У них есть и другие желательные свойства, о которых мы едва ли задумываемся. Например, никому и никогда не приходило в голову, что бильярдный шар может оказаться сразу в двух местах в один и тот же момент времени. Однако в квантовой механике такие явления вполне допустимы. Квантовомеханические системы, такие как в знаменитом эксперименте с двумя щелями, допускают, возможность одновременного присутствия фотона в двух местах (см. Э. Шимони. Реальность квантового мира, «В мире науки», 1988, № 3).

В нескольких словах: когда фотоны проходят через двойную щель, их можно рассматривать как волны, интерферирующие сами с собой. На экране позади щелей появляется интерференционная картина, если только мы не установим по детектору у каждой щели. Сам акт наблюдения как бы заставляет фотон решиться, через какую щель ему пройти! Это явление называется коллапсом вектора состояния. Эксперимент можно расширить для щелей, отстоящих друг от друга на километр (и даже на расстояние, равное световому году). Как утверждают многие физики, фотон может лишь в том случае решить, через какую щель ему пройти, если он по существу находится в обоих местах одновременно.

В какой точке бесконечного множества масштабов, от атомного до галактического, квантовомеханическая система становится классической? Эта дилемма иллюстрируется знаменитой кошкой Шредингера. В воображаемом эксперименте ученый, не страшащийся активистов движения в защиту животных, помещает кошку и сосуд с ядовитым газом в камеру, содержащую лазер, наполовину посеребренное зеркало, фотодетектор и молоточек. После того как дверь в камеру заперли, лазер испускает фотон по направлению к зеркалу. Если фотон проходит через него насквозь, кошке не причиняется никакого вреда. Если же фотон отражается от зеркала, он попадает в фотодетектор; последний приводит в действие молоточек, который ударяет по сосуду с газом и разбивает его; ядовитый газ убивает кошку. Находясь снаружи, мы не можем узнать, жива кошка или нет.

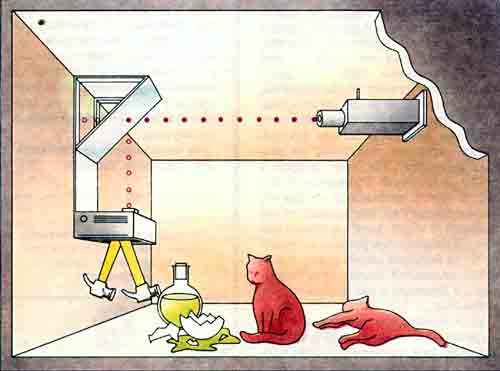
Кошка Шредингера - мертва, жива или и то и другое одновременно?

В мире квантовой механики два возможных события могут сосуществовать как суперпозиция двух реальностей. В классическом же мире может произойти либо одно, либо другое событие. Вектор состояния (а с ним, возможно, и жизнь кошки) должен претерпеть коллапс. По мнению Пенроуза, в современной теории отсутствует переходная область между классической физикой и квантовой механикой. Теория как бы расщепляется на две части, вместо того чтобы плавно переходить от одного масштаба к другому на всем их протяжении. Возможно, желаемый синтез будет получен с помощью теории квантовой гравитации.

Теперь вернемся, наконец, к человеческому разуму. Пенроуз полагает, что в человеческом сознании присутствует неалгоритмическая компонента. На квантовом уровне возможно сосуществование взаимоисключающих, альтернативных вариантов реальности. Одно квантовое состояние может в принципе состоять из большого количества различных, одновременно проходящих явлений. Может быть, человеческий мозг каким-то образом использует такие явления? Едва ли мне удастся проанализировать эту кажущуюся такой необычной возможность так же хорошо, как это делает Пенроуз. Поэтому я советую заинтересованным читателям приобрести и прочитать его книгу.

Однако у меня возникло желание рассмотреть другой вопрос, имеющий некоторое отношение к затронутой теме. Могут ли люди количественно оценить возможности своего интеллекта во Вселенной, которая обладает бесконечной структурой? В самом деле, существование какого-то определенного предела в структуре материи, будь то одна элементарная частица или набор таких частиц, кажется невероятным. При этом я имею в виду не только частицы, но вообще любую структуру, скажем энергетическую или чисто информационную, лежащую в основе обсуждаемых явлений.

Мне представляется, что физика сама по себе может оказаться бесконечной наукой по той простой причине, что, как только будет открыта какая-то предельная «элементарная» структура, сразу же возникнет проблема объяснения предельных элементарных законов и самого факта их существования. Во всяком случае, я предпочитаю жить во Вселенной, обладающей бесконечной структурой. Во-первых, наш разум мог бы лучше понять такую Вселенную по сравнению со Вселенной, которая обладает конечной структурой.

Компьютеры конструируются таким образом, чтобы исключить влияние любого физического процесса, протекающего на уровне, масштабы которого меньше определенного порога. Алгоритм должен быть защищен от «ошибок». Возможно, наш мозг структурирован так же, но, возможно, что и не так, считает Пенроуз. Не исключено, что физические явления, протекающие на атомарном уровне, играют важную роль в процессе нашего мышления. Что касается молекулярного уровня, то это определенно так. Достаточно лишь вспомнить о влиянии молекул нейротрансмиттеров на поведение нервных клеток. Более того, хорошо известно, что природа обладает свойством использовать физические возможности, ставя их на службу для реализации биологических операций. Если физические структуры простираются до определенного уровня, то имеем ли мы какие-то априорные основания полагать, что мозг не может воспользоваться явлениями, протекающими на этом уровне?

А что, если мозг способен пользоваться всеми уровнями структуры в бесконечно структурированной Вселенной? Чтобы продемонстрировать в самой грубой форме потенциальные возможности бесконечного мозга, я построил схему бесконечного компьютера, который пользуется в своей работе структурами всех уровней. В целях удобства демонстрации я буду условно считать, что во всех масштабах физические структуры обладают классическими свойствами.

Мой бесконечный компьютер по существу представляет собой квадрат, содержащий два прямоугольника и два других квадрата меньшего размера. Входная линия подведена слева к большому квадрату, и войдя в него, она сразу идет к первому прямоугольнику. Последний представляет собой устройство обработки сигналов, которое я назову модулем подстановки. От модуля подстановки отходит по одной линии к каждому из меньших квадратов, а также к другому прямоугольнику, который мы будем ниже называть модулем сообщения.

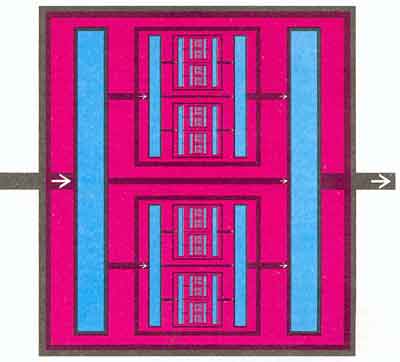
Фрактальный компьютер решает задачу Туэ о преобразовании слов

Структура этого компьютера обладает свойством бесконечной регрессии. Каждый из меньших квадратов является точной копией большего квадрата, но имеет вдвое меньшие размеры. Когда сигнал распространяется по проводникам и модулям вдвое меньшего размера, ему требуется вдвое меньше времени для прохождения соответствующего пути, поэтому модули подстановки и сообщения срабатывают в два раза быстрее соответствующих модулей внешнего уровня.

Бесконечный компьютер решает знаменитую задачу о преобразовании слов, изобретенную математиком Акселем Туэ. В этой задаче даны два слова и словарь допустимых подстановок. Можно ли, пользуясь только допустимыми подстановками, получить второе слово из первого? Рассмотрим задачу на следующем примере: предположим, первое «слово» представлено цепочкой 100101110, а второе - 01011101110. Возможно ли прийти от первого слова ко второму, пользуясь подстановками 010 вместо 110, 10 вместо 111 и 100 вместо 001? Пример был выбран совершенно произвольно, и я специально не буду пытаться решить его.

Может случиться так, что ни одна последовательность подстановок не приведет к преобразованию первой цепочки во вторую. В то же время такая последовательность существует. В процессе применения подстановок могут возникнуть очень длинные промежуточные слова. В этом и заключается проблема. Так же, как и в отношении некоторых точек множества Мандельброта, мы по существу не можем прийти к ответу. Не существует алгоритма решения этой задачи, поскольку любой алгоритм (по определению) должен когда-то остановиться. Опасность состоит в том, что алгоритм может остановиться прежде, чем будет получен ответ. По этой причине о задаче Туэ говорят как о неразрешимой. Ни одна компьютерная программа, даже в принципе, не сможет решить всех частных случаев этой задачи.

Введем условие задачи в бесконечный компьютер. Слово, к которому нужно прийти, вводится в компьютер через его главную входную линию. За четверть секунды оно попадает в первый подстановочный модуль. Затем слово передается этим подстановочным модулем двум другим подстановочным модулям следующего уровня.

Однако теперь передача данных потребует уже только 1/8 секунды. Пересылки на следующие уровни потребуют соответственно 1/16, затем 1/32 с и т.д. Время, которое потребуется, чтобы загрузить все подстановочные модули вторым словом, составит, таким образом, половину секунды.

Потом в ходе аналогичного процесса, протекающего с той же скоростью, в компьютер вводятся три (или сколько угодно) подстановочные формулы. Однако на этот раз различные подстановочные модули на разных уровнях запрограммированы так, чтобы воспринимать только определенные подстановки из вводимой последовательности. Каждый подстановочный модуль, согласно содержащейся в нем программе, должен всегда пытаться проводить определенную подстановку в определенной позиции слова, которое поступает в него из внешнего уровня. Подробное описание схемы распределения подстановок и позиций в слове по различным модулям, наверное, утомило бы читателя, поэтому я опускаю его. Однако это не должно помешать тем, кто любит анализировать бесконечные процессы, представить себе, каким образом можно все устроить.

Вычисление начинается, когда мы посылаем первое слово в компьютер. Первый подстановочный модуль пытается провести свою подстановку на отведенной для нее позиции введенного слова. Если подстановка не может быть выполнена в требуемом месте, слово передается следующему подстановочному модулю, принадлежащему более низкому уровню машины; если ему удается провести подстановку, он посылает преобразованное слово в квадрат более высокого уровня. Если подстановка оказывается успешной и полученное в результате слово совпадает со вторым заданным словом, хранящимся в памяти подстановочного модуля, то последний посылает сигнал модулю сообщения: «успешно».

Каждый квадрат каждого уровня работает в соответствии с только что описанным алгоритмом. Как уже говорилось выше, всегда можно распределить подстановки (и позиции, в которых их следует применять) по бесконечному компьютеру таким образом, чтобы задача преобразования слов успешно решалась. Ответ будет выдан не позднее чем через одну секунду: половина секунды потребуется, чтобы провести вычисления на всем пути до бесконечно малых модулей, и половина секунды на то, чтобы сообщение «успешно» достигло главной выходной линии компьютера. Если подходящей последовательности подстановок не существует, то отсутствие сообщения по истечении одной секунды можно принять как ответ «нет». Читателям, возможно, будет интересно поразмыслить над бесконечным компьютером, воспользовавшись при этом многочисленными (а может быть, и бесконечным числом) структурами своего собственного мозга.

В МИРЕ НАУКИ. (Scientific American. Издание на русском языке). 1990. № 12 стр. 6-13.

Шахматная машина - гроссмейстер

Сорок лет назад в журнале "Scientific American" была опубликована статья с описанием оригинального проекта шахматного компьютера. С тех пор машины побеждали сначала новичков, затем мастеров, а теперь уже и гроссмейстеров. Будет ли следующим Гарри Каспаров?

ФЭН-СЮН СЮЙ, ТОМАС АНАНТАРАМАН, МЮРРЕЙ КЭМПБЕЛЛ, АНДРЕАС НОВАЦИК

В ЯНВАРЕ 1988 г. на пресс-конференции в Париже чемпиона мира по шахматам Гарри Каспарова спросили, сумеет ли компьютер выиграть у гроссмейстера до 2000 года? «Ни в коем случае, - ответил он, - и если у кого-нибудь из гроссмейстеров возникнут затруднения в игре с компьютером, я с удовольствием дам им совет».

ЧЕМПИОН МИРА Гарри Каспаров и компьютер IBM PS/2, с помощью которого осуществляется связь с «Глубокой мыслью», перед началом матча против машины, состоявшегося в конце 1989 г. Каспаров победил, несмотря на гроссмейстерский рейтинг «Глубокой мысли».

Спустя 10 месяцев после заявления Каспарова, на крупном турнире, состоявшемся в Лонг-Биче (шт. Калифорния), гроссмейстер БентЛарсен, в прошлом претендент на мировую корону, потерпел поражение в поединке с играющей машиной, которую мы сконструировали в качестве своего аспирантского проекта в Университете Карнеги - Меллона. Машина, представляющая собой сочетание программ и специализированной аппаратуры и названная "Deep Thought" («Глубокая мысль»), выиграла еще 5 встреч, одну проиграла и одну свела вничью, разделив с гроссмейстером Энтони Майлсом первое место на турнире. Поскольку машинам не присуждается денежная премия за победу в турнире, Майлс положил в свой карман первый приз в размере 10 тыс. долл. («Глубокая мысль» все же победила Майлса через год в показательном матче.)

К лету 1990 г., когда трое из нас поступили на службу в корпорацию IBM, «Глубокая мысль» достигла 50%-ного успеха в 10 встречах с гроссмейстерами и 86%-ного успеха в 14 играх против мастеров международного класса. Некоторые из числа этих матчей, а также десятки других игр, сыгранных против менее именитых соперников, проходили под эгидой шахматной федерации США, которая по результатам игр определила шахматный рейтинг машины. Он оказался равным 2552. Этот рейтинг соответствует уровню нижней половины гроссмейстерского диапазона. В то же время средний турнирный игрок имеет рейтинг примерно 1500 очков). Теперь, когда компьютер достиг своей нынешней скорости анализа ситуаций на доске - 750 тыс. позиций в секунду, - рейтинг машины еще более возрос и превысил 2600.

Машина следующего поколения, которая, как ожидается, сыграет свою первую партию в 1992 г., будет обладать значительно более мощными аппаратными средствами. Быстродействие при анализе ситуаций возрастет более чем в 1000 раз и выйдет на уровень примерно одного миллиарда позиций в секунду. Благодаря только этой способности «Глубокая мысль», вполне возможно, станет играть в шахматы сильнее Каспарова или любого другого даже более способного шахматиста, если такой появится.

Зачем же потребовалось учить машину загонять в угол деревянного короля на шахматной доске? Во-первых, шахматы всегда рассматривались в традициях западной культуры как изысканная игра разума и, по словам Гете, «как пробный камень интеллекта». Многие люди утверждают, что успех машины в шахматной игре послужит доказательством того, что человеческое мышление можно смоделировать, или же, наоборот, что шахматы не требуют мышления как такового. В любом случае, однако, тот или иной вывод значительно изменит наши представления о том, что мы обычно называем интеллектом.

С другой стороны, создание компьютера, умеющего играть в шахматы, представляет собой увлекательную техническую проблему. Она была описана на страницах журнала "Scientific American" 40 лет назад Клодом Шенноном, основоположником теории информации (см.: Shannon С.Е., A Chess-Playing Machine, "Scientific American", February, 1950). Приведем выдержку из этой статьи:

Цель исследований, связанных с созданием шахматной машины, заключается в том, чтобы разработать техническое средство, которое можно было бы применить в практически более важных приложениях. Построение шахматной машины является идеальным началом по нескольким причинам. Задача строго определена как в смысле дозволенных операций (шахматные ходы), так и в смысле конечной цели (поставить «мат» королю). Она не настолько проста, чтобы быть тривиальной, но и не настолько трудна, чтобы не поддавалась решению. Кроме того, такая машина могла бы соревноваться с человеком, что позволило бы однозначно судить о способности машины к логическим рассуждениям подобного типа.

По-видимому, наиболее важное практическое значение разрабатываемых шахматных программ заключается в демонстрации эффективности выбираемых методов компьютерного анализа. Усовершенствование используемых в этих программах методов обещает определенный прогресс в конструировании сетей, моделировании химических реакций и даже лингвистическом анализе.

ПЕРВАЯ попытка практически реализовать идею создания играющей в шахматы машины была предпринята в 60-х годах XVIII в., когда барон Вольфганг фон Кемпелен начал демонстрировать свой шахматный автомат, разъезжая по Европе. Машину прозвали «турком», поскольку ходы на доске выполняла усатая кукла с тюрбаном на голове, которая, очевидно, приводилась в движение замысловатым механизмом, спрятанным в основании машины. Обычно машина играла довольно хорошо и однажды привела в бешенство Наполеона Бонапарта, выиграв у него за 19 ходов. Эдгар Алан По, как и многие другие, впоследствии разгадал секрет автомата: его ходы делал опытный шахматист карликового роста, скрытый в потайном отделении. Однако По неправильно аргументировал свою догадку: по его мнению, эпизодические проигрыши «турка» находились в противоречии с предполагаемым совершенством, присущим настоящему автомату.

Алан М. Тьюринг, английский математик, пионер информатики и специалист в области криптографии, был в числе первых, кто начал рассматривать перспективу создания компьютера, играющего в шахматы. Однако ему было легче разработать свою простую программу, генерирующую ходы и оценивающую позиции на доске, при помощи карандаша и бумаги, чем прибегнуть к помощи компьютера. Аналогичные попытки совершали Конрад Цузе в Германии и другие ученые, однако основополагающая работа была выполнена Шенноном. Ему удалось развить идеи Джона фон Неймана и Оскара Моргенштерна, которые в рамках своей универсальной теории игр изобрели так называемый минимаксный алгоритм, позволяющий вычислять наилучший ход в заданной ситуации.

Эта процедура определенным образом представляет произвольно большое число позиций, могущих возникнуть в результате каждой возможной последовательности ходов, ставит им в соответствие некую числовую оценку и затем движется в обратном направлении, отправляясь от этих конечных оценок, чтобы выбрать наилучший первый ход. Процедура начинает свою работу после того, как генератор ходов получит все ходы, которые компьютер может сделать в данной позиции, затем все возможные ходы противника и т.д. Каждый шаг по цепочке событий на доске называется полуходом в шахматной терминологии или слоем в терминологии теории игр.

Каждый новый слой в ветвящемся дереве анализа охватывает приблизительно в 38 раз большее количество позиций (среднее количество ходов в шахматной позиции), чем предыдущий слой, или в 6 раз большее количество позиций в случае, когда используется метод «альфа-бета-усечения» (см. диаграмму). Поэтому большинство возможных позиций находится на самых внешних частях ветвей дерева игры, «наращиваемых» до тех пор, пока не кончится игра, или время, отпущенное компьютеру, не будет исчерпано. Оценивающий функционал присваивает каждой конечной позиции определенное числовое значение, например 1 для позиции «мат» противнику, - 1 для позиции, в которой выигрывает противник, и 0 для ничейного исхода. Можно регистрировать также и менее явные преимущества и недостатки позиций. Например, компьютер может подсчитывать материальный баланс, выражаемый в количестве фигур и пешек, и вычислять оценку позиций с учетом расположения фигур на доске, положения пешек, занятия ими свободной вертикали, контроля за центральной частью доски и т.д.

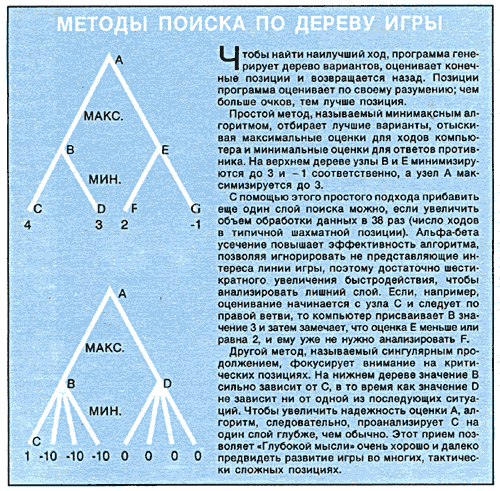
Чтобы найти наилучший ход, программа генерирует дерево вариантов, оценивает конечные позиции и возвращается назад. Позиции программа оценивает по своему разумению; чем больше очков, тем лучше позиция.

Простой метод, называемый минимаксным алгоритмом, отбирает лучшие варианты, отыскивая максимальные оценки для ходов компьютера и минимальные оценки для ответов противника. На верхнем дереве узлы В и Е минимизируются до 3 и -1 соответственно, а узел А максимизируется до 3.

С помощью этого простого подхода прибавить еще один слой поиска можно, если увеличить объем обработки данных в 38 раз (число ходов в типичной шахматной позиции). Альфа-бета усечение повышает эффективность алгоритма, позволяя игнорировать не представляющие интереса линии игры, поэтому достаточно шестикратного увеличения быстродействия, чтобы анализировать лишний слой. Если, например, оценивание начинается с узла С и следует по правой ветви, то компьютер присваивает В значение 3 и затем замечает, что оценка Е меньше или равна 2, и ему уже не нужно анализировать F.

Другой метод, называемый сингулярным продолжением, фокусирует внимание на критических позициях. На нижнем дереве значение В сильно зависит от С, в то время как значение D не зависит ни от одной из последующих ситуаций. Чтобы увеличить надежность оценки А, алгоритм, следовательно, проанализирует С на один слой глубже, чем обычно. Этот прием позволяет «Глубокой мысли» очень хорошо и далеко предвидеть развитие игры во многих, тактически сложных позициях.

Можно усилить игру компьютера, повышая его способность к поиску или улучшая чувствительность к факторам, влияющим на оценку позиции. Безупречной игра компьютера будет в том случае, когда он сумеет генерировать все возможные направления развития игры вплоть до конечных позиций, в которых либо машина, либо ее противник попадут в матовую ситуацию или игра закончится вничью. Такой компьютер мог бы удивить своего противника, объявив на первом же ходе: «Белые начинают и выигрывают на 137 ходу» или же, наоборот, сдавшись в неочевидной позиции, признав ее как безнадежную. Подобный исчерпывающий анализ не представляет серьезных затруднений в таких простых играх, как «крестики-нолики», но неосуществим в шахматах, допускающих 10^120 различных развитии игры. В одинаковой степени совершенной игра могла бы стать и при исследовании только одного слоя игры при условии, что оценка позиций настолько же хороша, насколько ее можно охарактеризовать словами Ричарда Рети, шахматного мастера, успешно выступавшего в 20-х годах, когда он сказал, что видит игру лишь на один ход вперед - наилучший.

ОЧЕНЬ далеко до таких заявлений было тем программистам, которые первыми пытались создавать шахматные программы. До 1958 г. они даже не могли научить машину строго соблюдать правила игры. Прошло еще восемь лет, прежде чем программа "МасНаск-6", написанная Ричардом Д.Гринблаттом из Масса-чусетского технологического института, впервые достигла уровня средних турнирных игроков.

По мере того как число людей, занимавшихся шахматными программами, росло, они стали делиться на два лагеря. Назовем их условно лагерем моделирования и техническим лагерем. Сторонники первого направления утверждали, что компьютеры должны играть так же, как люди, и быть способными логически «рассуждать» при выборе хода. Представители другой группы придерживались менее строгих требований к компьютеру. То, что хорошо для людей, говорили они, может оказаться неприменимым для компьютера. Сторонники моделирования имели преимущество на начальном этапе, пока компьютерные шахматы оставались скорее теорией, чем практикой.

В 70-х годах технический лагерь вышел на первый план, когда выяснилось, что глубина анализа игровой ситуации почти линейно коррелирует с рейтингом шахматной программы. Каждый дополнительный слой анализа прибавлял примерно 200 очков в оценке способностей компьютера. Поэтому программисты стали обращаться ко все более быстродействующим машинам и изобретать различные технические уловки, позволявшие добиться большей глубины анализа при доступных вычислительных мощностях.

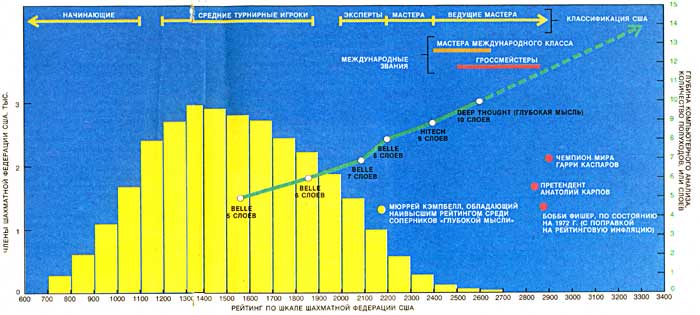
ВОЗРАСТАЮЩАЯ СИЛА компьютеров проявляется при наложении рейтингов 35 тыс членов шахматной федерации США и машин, обладающих различной глубиной анализа (зеленый). Компьютеры приобретают примерно по 200 очков на каждый дополнительный полуход, или слой игры, который они анализируют. Сейчас «Глубокая мысль» исследует 10 слоев и имеет рейтинг примерно 2600 очков. Ее преемница будет способна анализировать 14 или 15 слоев, и ее рейтинг будет намного выше.

Однако глубокий анализ - это лишь полдела. В самом начале шахматного программирования программы поиска лучшего хода генерировали позиции практически без всякого их анализа. Вариации, ведущие к одной и той же позиции, они рассматривали как различные ветви в процессе поиска. Такое излишнее дублирование теперь блокируется путем слежения за позициями в массивах памяти, известных под названием кэш-таблиц. Кэш-таблицы обеспечивают еще большее преимущество, помогая альфа-бета-алгоритму отбрасывать многие не представляющие интереса ветви в развитии игры.

Важнейшая проблема в анализе возможных ситуаций и поиске наилучшего хода - это умение определить, в какой момент следует прекратить анализ бесчисленных ветвей игрового дерева. Невозможно исследовать все ветви до конца, но желательно не прекращать анализа по крайней мере в нестабильной позиции. Такие ситуации могут, например, возникать, когда анализ прекращается в процессе размена фигур. Предположим, что компьютер просматривает все ветви вперед ровно на восемь уровней и доходит до позиции, в которой он на этом восьмом уровне, кажется, выигрывает коня в обмен на пешку. Даже в том случае, если противник следующим ходом вернет себе коня и сохранит преимущество в одну пешку, компьютер все-таки будет стремиться к этой позиции, дающей ему мнимое материальное преимущество.

Этот так называемый эффект горизонта может вынудить компьютер совершить своеобразное шахматное самоубийство, чего нельзя ожидать при игре даже самого слабого игрока с сильным. Совершенно неожиданно и, казалось бы, без всякой причины с точки зрения наивного наблюдателя машина начинает раздавать свои пешки и фигуры, безнадежно ухудшая свою позицию. Чтобы снизить вероятность подобных ошибок, практически во всех шахматных программах дополнительно к основному анализу предусматривается стадия стабилизирующего анализа. При таком дополнительном анализе исследуются лишь те последовательности ходов, в которых теряются или приобретаются пешки и фигуры, и поиск хода продолжается до тех пор, пока не будет достигнута стабильная позиция, легко поддающаяся оценке при помощи статических параметров.

В 70-е и 80-е годы доминировали так называемые «силовые» машины (brute-force machine), поскольку эффективность их игры в основном определялась замысловатой реализацией стратегии основного и стабилизирующего анализа. Почти весь этот период проходил под знаком превосходства программы Северо-западного университета "Chess 4.0" и программ из серии «4-Х», которые последовали за ней. Программа Северозападного университета переходила с одного поколения компьютерной аппаратуры на другое, постоянно увеличивая свой рейтинг, пока он не превзошел мастерского уровня (2000 очков) в 1979 г.

В 70-х годах было сделано также несколько первых попыток создания специализированных шахматных машин. Наиболее известная из этих машин, созданная в компании AT&T Bell Laboratories и названная "Belle", преодолела в 1983 г. барьер в 2200 очков, соответствующий уровню мастера в американской шахматной федерации. Эра чисто силовых машин достигла своего апогея в 1986 г., когда на шахматной арене появилась программа "Cray Blitz", выполняющаяся на суперкомпьютерах серии "Cray", а также система "Hitech" - специализированная шахматная машина, генерировавшая ходы на 64 процессорных микросхемах, по одной на каждую клетку игрового поля. "Hitech" выиграла чемпионат Северной Америки по шахматам среди компьютеров в 1985 г., а "Cray Blitz" победила на чемпионате мира 1986 г., выиграв в дополнительном матче у "Hitech", так сказать, в последнем раунде. "Cray Blitz" и "Hitech" анализировали соответственно 100 и 120 тыс позиций в секунду.

У «Глубокой мысли» довольно необычная история. Во-первых, она разрабатывалась группой выпускников университета, не имевших официальной финансовой поддержки или прямого руководства на факультете. (Сотрудники факультета, занимавшиеся в Университете Карнеги - Меллона исследованиями в области шахматных программ, не сотрудничали с группой разработчиков «Глубокой мысли».) Во-вторых, члены группы специализировались до этого в разных областях и потому их подходы часто оказывались нетрадиционными.

В ИЮНЕ 1985 г. один из нас (Сюй) пришел к выводу, что можно создать генератор ходов в виде единого процессора на базе сверхбольших интегральных микросхем (СБИС), поставляемых научным учреждениям Агентством по научно-исследовательским разработкам в области обороны (DARPA). Сюй построил генератор ходов на базе системы "Belle", придумав несколько усовершенствований, благодаря которым устройство можно было реализовать в единой микросхеме очень высокой степени интеграции. Ему удалось также сконструировать кристалл таким образом, чтобы эффективно расположить его электронные элементы (включая 35 925 транзисторов), несмотря на то, что самые мелкие элементы имели довольно большие размеры (3 мкм). Изготовление кристалла с элементами указанного размера взяла на себя фирма MOSIS, работающая по контракту с агентством DARPA. Сюй затратил шесть месяцев на конструирование, моделирование и разводку микросхемы, после чего прошло еще четыре месяца, прежде чем он получил первые рабочие образцы устройства. Он проверил работу процессора, подключив его к компьютерной рабочей станции,и установил, что устройство способно обрабатывать до двух миллионов ходов в секунду, т.е. в 10 раз быстрее, чем матрица "Hitech", состоявшая из 64 микропроцессоров.

После этого Сюй привлек к проводимой им работе Т. Анантарамана - аспиранта с факультета информатики, специализировавшегося на распознавании речи. Анантараман написал небольшую шахматную программу, генерировавшую ходы на основе программного моделирования. Заменив программный модуль генерирования ходов тестером Сюя, Анантараман повысил скорость анализа программы в пять раз, и в результате быстродействие шахматной машины увеличилось до 50 тыс. позиций в секунду.

Сюй и Анантараман были полны честолюбивых замыслов и, не долго думая, решили подготовить свою машину к Североамериканскому чемпионату по шахматам среди компьютеров 1986 г., который должен был начаться всего через семь недель. К проекту были привлечены еще два аспиранта, М. Кэмпбелл и А. Новацик, также с факультета информатики. Задача заключалась в том, чтобы построить более совершенный оценивающий функционал, и Кэмпбелл, ранее принимавший участие в шахматных соревнованиях, согласился попробовать свои силы. Вторая, и более трудная, задача, учитывая ограничения во времени, состояла в расширении функции тестера микросхем так, чтобы он мог играть роль простой анализирующей машины. Такая машина должна была полнее использовать потенциальные скоростные возможности микросхемы генератора ходов по сравнению с рабочей станцией.

Сюй принял решительные меры, чтобы вовремя подготовить технику: он решил, что его машина будет игнорировать две шахматные ситуации - рокировку и повторение позиций. (Игрок может настоять на ничейном результате, если докажет, что определенная позиция трижды повторена в игре и ходить в этой позиции должен тот же игрок.) Чтобы компенсировать этот недостаток, была принята гибридная стратегия поиска, согласно которой ранние слои игрового дерева анализировались управляющим компьютером, учитывавшим рокировку и повторение позиций. Последующие слои (включающие, конечно, большую часть возможных позиций) анализировались уже специализированной машиной поиска.

Мы не располагали никакими денежными средствами и поэтому собрали нашу первую машину "ChipTest" из деталей, заимствованных из других проектов. Суммарная стоимость всех компонентов не превышала 500 или 1000 долл. с учетом ориентировочной стоимости кристаллов, производство которых финансировалось агентством DARPA. Однако ни аппаратура поисковой машины, ни программное обеспечение управляющего компьютера не были полностью отлажены к началу чемпионата, и не лишенная недостатков машина сумела добиться на турнире лишь ничейного результата. Тем не менее это было немалым достижением если учесть, что вся работа была проделана в течение семи недель.

Этот дебют научил нас многому. Например, Сюй подметил, что две другие программы избрали такую тактику, при которой каждый их ход был вынужденным и ни одна из сторон заранее не предвидела исхода игры. Другими словами, программа, добившаяся лучшей позиции, достигала этого благодаря чисто случайным факторам. Сюй предложил исправить этот дефект при помощи приема, названного им алгоритмом сингулярного продолжения. Алгоритм как бы заглядывает глубже, т.е. продолжает анализ на большей глубине, в тех ситуациях, когда компьютер «видит» лишь один хороший ход. В данном случае цель заключалась в том, чтобы особое внимание обращалось на критические позиции.

Когда одна сторона близка к выигрышу, скажем слон противника попал в безвыходное положение, у защищающегося по мере углубления анализа остается все меньше и меньше хороших ответных ходов. В конце концов остается лишь один хороший ход, после которого слон все же оказывается потерянным. В подобных случаях в бой вступает сингулярное продолжение. Благодаря ему в одной из игр компьютер привел мастера в состояние шока, объявив ему форсированный мат за 19 ходов.

Анантараман, единственный член группы, умевший программировать управляющий компьютер системы "ChipTest", написал программу, реализующую алгоритм сингулярного продолжения. Тем временем Сюй завершил написание микропрограмм, управляющих аппаратурой на самом низшем уровне. Анализируя от 400 до 500 тыс позиций в секунду, система "ChipTest" выиграла чемпионат Северной Америки по шахматам среди компьютеров в 1987 г., победив всех своих соперников, в том числе машину, носившую титул чемпиона мира, - "Cray Blitz". Таким образом закончилась эпоха чисто силовых машин. Сейчас почти все сильнейшие программы содержат по крайней мере некоторые элементы выборочного анализа.

Наш опыт показал, что быстродействие системы "ChipTest" можно повысить еще больше, а анализ проводить, так сказать, более разумно. Первоначальное финансирование этого проекта, теперь называющегося «Глубокая мысль», было предоставлено X. Кунгом, консультантом Сюя.

Шахматная машина «Глубокая мысль» в своем основном варианте содержит 250 микросхем, включая два процессора, установленные на одной плате, размерами в половину формата этого журнала. Машина управляется программой, так называемым управляющим программным обеспечением, выполняющейся на компьютере рабочей станции. Процессоры машины едва ли обладают более высоким физическим быстродействием по сравнению с системой "ChipTest", однако усовершенствованное управление алгоритмом анализа позволяет им проводить поиск лучшего хода на 30% эффективнее.

СЕРДЦЕ «Глубокой мысли» помещается на плате размером с большую пиццу. Каждый из двух ее процессоров способен анализировать 500 тыс позиций в секунду. Машина следующего поколения превратит «Глубокую мысль» в одну микросхему; в ней 1000 таких процессоров будут работать параллельно.

Оценочное устройство состоит из четырех компонентов. Оценка расположения фигур (единственная операция, перешедшая по наследству от системы "ChipTest") базируется на близости фигуры к центру доски, на ее подвижности и других соображениях. Размещение пешек оценивается в зависимости от таких параметров, как их взаимная поддержка, контроль за цетральной частью доски и способность защитить короля. Оцениваются также так называемые проходные пешки, которым не препятствуют пешки противника и поэтому они могут пройти до восьмого ряда и превратиться в ферзя. Проводится еще и дополнительная оценка, учитывающая более сложные позиции пешек и ладей на определенной линии.

Мы начали также работу по настройке примерно 120 параметров оценивающего функционала, фигурирующих в нашем программном обеспечении. Как правило, шахматные мастера вручную настраивали весовые коэффициенты, приписываемые программой материальным факторам (пешкам и фигурам) и позиционным показателям. По нашему мнению, мы располагаем единственной добротной программой, которая настраивает свои весовые коэффициенты автоматически.

МЫ ОТОБРАЛ И 900 игр с участием мастеров для анализа и произвольно определили оптимальные веса, которые обеспечивают наилучшее соответствие между ходами, получившими наиболее высокую оценку у машины, и ходами, в действительности сделанными мастерами. Оценивающая часть программного обеспечения была полностью переписана Кэмпбеллом и Новациком с целью реализации этой стратегии. Вместо того чтобы однозначно присваивать определенное численное значение каждой позиции, оценочная функция, работающая в режиме настройки, возвращает цепочку линейных членов. Другими словами, она вычисляет вектор.

Было применено два механизма настройки. При использовании первого метода, который мы называем методом подъема, данный оценочный параметр просто устанавливается в произвольное значение, а затем проводится анализ на глубину, скажем, пяти или шести уровней для каждой позиции, содержащейся в игровой базе данных, чтобы найти ходы, которые сделала бы машина. После этого в значение параметра вносится поправка и проводится перерасчет. Если количество совпадений между ходами компьютера и гроссмейстера возрастает, параметр опять корректируется в том же направлении. Процесс продолжается до тех пор, пока все параметры не достигнут оптимального значения, или высшего уровня эффективности. Однако чтобы с помощью этого метода оптимизировать все параметры, потребуются годы, поэтому мы воспользовались им лишь в нескольких сложных случаях.

Второй метод настройки, предложенный и реализованный Новациком, работал значительно быстрее. Он сформировался в процессе того, как мы пытались найти наилучшее соответствие между функцией оценки позиций, применяемой машиной, и предположительно верными их значениями. Наилучшее соответствие получается при наименьшем среднеквадратичном отклонении между моделью и истинными значениями. Истинные значения можно приблизительно вычислить по результатам глубокого поиска (если тонкой настройке подвергается какая-то конкретная, известная оценочная компонента) или путем сравнения решений, принятых машиной, с ходами, выбранными первоклассными игроками в аналогичной ситуации.

Образцы партий, сыгранных мастерами, дают хороший критерий для относительной оценки позиций: любая позиция, полученная в результате хода гроссмейстера, с большой вероятностью будет лучше любой другой позиции, возникающей в результате альтернативного хода. Вместо того чтобы вычислять оценку позиции по ее параметрам, Новацик рассчитывал параметры, основываясь на предполагаемой разнице между позицией, выбранной гроссмейстером, и альтернативными позициями, которые были им отвергнуты. Вычисления по его алгоритму выполняются всего за несколько дней, но в отличие от метода подъема он не позволяет оптимизировать значения конкретных параметров. Скорее, с помощью этого метода повышается общая эффективность всего набора параметров.

Наша автоматически настраиваемая оценочная функция, пожалуй, не хуже, если не лучше настроенных вручную функций в таких знаменитых академических шахматных программах, как "Hitech" и "Cray Blitz". Однако, по-видимому, все же остается разрыв между оценочной функцией «Глубокой мысли» и лучшими коммерческими образцами шахматных машин, создание которых потребовало многих человеко-лет. Мы надеемся в недалеком будущем преодолеть этот разрыв за счет усовершенствования обратных связей в процедурах автоматической настройки.

Может показаться странным, что наша машина, вмещающая относительно небольшой объем знаний об игре в шахматы, все же обыгрывает первоклассных игроков. Однако не следует забывать, что компьютер не моделирует человеческое мышление, он достигает того же эффекта за счет других средств. «Глубокая мысль» способна проследить игру на много ходов вперед, но замечает мало; помнит все, но ничему не учится; не совершает грубых ошибок, но и не превосходит саму себя в минуты вдохновения. И тем не менее она иногда находит решения, которые ускользают от внимания даже сильнейших гроссмейстеров.

Возможно, именно этот нестандартный, отличный от присущего человеку взгляд на игру, свойственный машине, привлек внимание гроссмейстера Кевина Спрэггета, решившего потренироваться с помощью машины перед четвертьфинальным матчем претендентов т.а звание чемпиона мира с гроссмейстером Артуром Юсуповым. Участие машины не оказало заметного влияния на матч, но все же имел место один интересный прецедент.

В октябре 1989 г. «Глубокая мысль» в экспериментальной шестипроцессорной версии сыграла показательный матч из двух партий против Каспарова. Матч проходил в Нью-Йорке. Хотя новая версия могла «просматривать» более двух миллионов позиций в секунду, Каспаров довольно легко с ней справился. Результат не был неожиданным, но игра «Глубокой мысли» оказалась, пожалуй, разочаровывающей.

В феврале нынешнего года «Глубокая мысль» провела показательную игру с Анатолием Карповым - бывшим чемпионом мира и соперником Каспарова в матче за звание чемпиона мира, который начался в октябре 1990 г. в Нью-Йорке и завершится во Франции в Лионе. Дефекты, выявленные в экспериментальном программном обеспечении шести- и четырехпроцессорной версий, заставили нас вернуться к двухпроцессорной версии. Благодаря ряду усовершенствований в оценочной функции «Глубокая мысль» сыграла одну из лучших своих игр в течение первых 50 ходов, но затем, совершив досадную ошибку, упустила явную ничью. У стабильной шестипроцессорной версии хватило бы скорости, чтобы избежать этой ошибки:

БЫСТРОДЕЙСТВИЕ является ключевым фактором в работе, проводимой сейчас в Исследовательском центре им. Томаса Дж.Уотсона фирмы IBM, где конструируется машина следующего поколения. По скорости вычислений она будет превосходить свою предшественницу по крайней мере в 1000 раз. Задуманная нами машина, таким образом, будет анализировать более миллиарда позиций в секунду. Этого будет достаточно, чтобы проводить поиск на 14 или 15 слоев в большинстве случаев и от 30 до 60 слоев в критических ситуациях. Если наблюдавшаяся до сих пор связь между быстродействием и качеством игры сохранится, то машина следующего поколения будет играть на уровне мастера с рейтингом 3400 очков, по крайней мере на 800 очков превосходящий сегодняшний рейтинг «Глубокой мысли» и на 500 - рейтинг Каспарова.

Чтобы достичь такой скорости, Сюй конструирует специализированный шахматный микропроцессор, который по проектным данным должен генерировать по меньшей мере 3 млн ходов в секунду, что более чем в три раза превосходит возможности нынешней версии «Глубокой мысли». Одновременно он разрабатывает вычислительную систему с высокой степенью параллелизма, в которой объединяется мощность более тысячи таких процессоров, что обеспечит дополнительный прирост скорости приблизительно еще в 300 раз. Анантараман и Кэмпбелл заняты усовершенствованием ряда аспектов нынешней версии «Глубокой мысли», с тем чтобы эти усовершенствования также «встроить» в машину следующего поколения. Новацик теперь увлечен другими идеями.

Мы полагаем, что за счет одной только скорости наша система сможет стать достойным соперником чемпиона мира. Мы считаем также, что благодаря большому числу других запланированных усовершенствований машина получит преимущество, возможно, уже в 1992 г.

Ну что ж, Каспаров задал нам работы, и мы должны прислушиваться к его мнению. Возможно, он только сейчас всерьез занялся изучением сильных и слабых сторон, присущих шахматным машинам. В частной беседе Каспаров признал, что машина, анализирующая миллиард позиций в секунду, способна побеждать гроссмейстеров среднего уровня, добавив, однако: «Но не Карпова и не меня!». Он утверждает, что творчество и воображение человеческого ума, а в особенности его собственное творчество и воображение, определенно должны оказаться сильнее простого кремниевого кристалла и соединительных проволочек.

Однако в действительности за шахматной доской столкнутся два подхода - изобретательность одного, в высшей степени талантливого, человека будет противопоставлена работе нескольких поколений математиков, электронщиков и программистов. Мы считаем, что результат поединка между нынешним чемпионом мира и компьютером не ответит на вопрос, может ли машина мыслить, а скорее покажет, могут ли усилия коллектива людей превзойти достижения одной, пусть даже наиболее талантливой, личности.

К оглавлению

(Последние исправления - 28.3.2002)